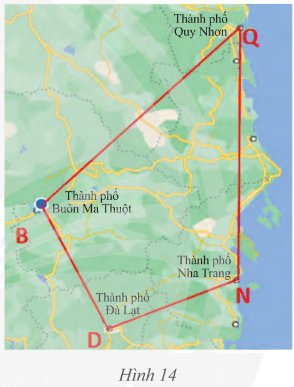
Trên bản đồ, tứ giác \(BDNQ\) với các đỉnh là các thành phố Buôn Ma Thuột, Đà Lạt, Nha Trang, Quy Nhơn.
a) Tìm các cạnh kề và cạnh đối diện của cạnh \(BD\).
b) Tìm các đường chéo của tứ giác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Xác định các thành phố: Play – Ku , Buôn Ma Thuật, Đà Lạt trên hình 29.2
- Những quốc lộ nối các thành phố này với Thành phố Hồ Chí Minh và các cảng biển của vùng Duyên hải Nam Trung Bộ:
- Quốc lộ 19: Kom Tum - Quy Nhơn.
- Quốc lộ 26: Buôn Ma Thuột - biến Nha Trang.
- Quốc lộ 14 và đường Hồ Chí Minh nối Plây Ku, Buôn Ma Thuột với TP. Hồ Chí Minh.



ĐỈnh: C, H, R, L
Đường chéo: CR, HL
Cạnh: CH, HR, RL, CL

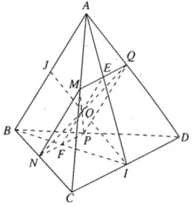
a) 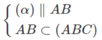
⇒ (α) ∩ (ABC) = MN và MN // AB
Ta có N ∈ (BCD) và 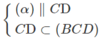
Nên ⇒ (α) ∩ (BCD) = NP và NP // CD
Ta có P ∈ (ABD)
Và 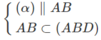 nên ⇒ (α) ∩ (ABD) = PQ và PQ // AB
nên ⇒ (α) ∩ (ABD) = PQ và PQ // AB
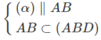 nên ⇒ (α) ∩ (ACD) = MQ và MQ // CD
nên ⇒ (α) ∩ (ACD) = MQ và MQ // CD
Do đó MN // PQ và NP // MQ, Vậy tứ giác MNPQ là hình bình hành.
b) Ta có: MP ∩ NQ = O. Gọi I là trung điểm của CD.
Trong tam giác ACD có : MQ // CD ⇒ AI cắt MQ tại trung điểm E của MQ.
Trong tam giác ACD có : NP // CD ⇒ BI cắt NP tại trung điểm F của NP.
Vì MNPQ là hình bình hành nên ta có
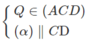
EF // MN ⇒ EF // AB
Trong ΔABI ta có EF // AB suy ra : IO cắt AB tại trung điểm J
⇒ I, O, J thẳng hàng
⇒ O ∈ IJ cố định.
Vì M di động trên đoạn AC nên Ochạy trong đoạn IJ .
Vậy tập hợp các điểm O là đoạn IJ.

Xét tứ giác ABCD có cạnh đối diện AD và BC cắt nhau tại O. Gọi D1 và C1 lần lượt là các điểm đối xứng của C và D qua O. Khi đó có :
\(AC_1=AC,BD_1=BD,C_1D_1=CD\)
Áp dụng định lí ta có:
\(ABD_1C_1:AD_1\perp BC_1\Leftrightarrow AB^2+C_1D_1^2=AC^2_1+BD^2_1\)
\(\Rightarrow AD\perp BC\Leftrightarrow AB^2+CD^2=AC^2+BD^2\)
a) Các cạnh kề của \(BD\) là: \(BQ\), \(DN\)
Cạnh đối của cạnh \(BD\) là: \(NQ\)
b) Các đường chéo của tứ giác là: \(BN;\;DQ\)