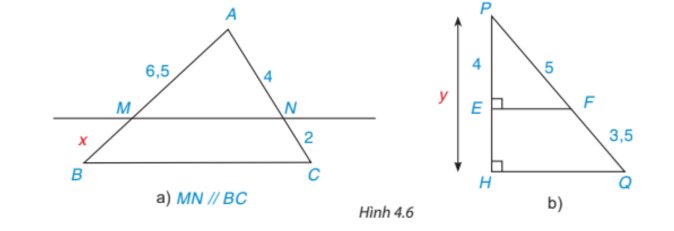
Tìm các độ dài x, y trong Hình 4.6.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng định lí tổng ba góc trong tam giác, ta có:
+)
\(\begin{array}{l}x + {120^o} + {35^o} = {180^o}\\ \Rightarrow x + {155^o} = {180^o}\\ \Rightarrow x = {180^o} - {155^o}\\ \Rightarrow x = {25^o}\end{array}\)
+)
\(\begin{array}{l}y + {70^o} + {60^o} = {180^o}\\ \Rightarrow y = {180^o} - {70^o} - {60^o}\\ \Rightarrow y = {50^o}\end{array}\)
+)
\(\begin{array}{l}z+ {90^o} + {55^o} = {180^o}\\ \Rightarrow z = {180^o} - {90^o} - {55^o}\\ \Rightarrow z = {35^o}\end{array}\)

x=180-120-35=180-155=25 độ
y=180-70-60=50 độ
z=180-90-55=35 độ

Áp dụng hệ quả của định lí Ta – lét ta có:
DE//BC ⇒ BC/DE = AB/AD hay x/8 = 28,5/9,5
⇔ x = (8.28,5)/9,5 = 456/19 ≈ 31,58

Ta có: A'B'//AB vì cùng vuông góc AA'
Áp dụng hệ quả của định lí Ta – lét ta có:
A'B'//AB ⇒ AB/A'B' = AO/A'O hay x/4,2 = 6/3 ⇔ x = 8,4
Áp dụng định lí Py – ta – go với Δ OAB ta có:
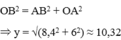

Áp dụng hệ quả của định lí Ta – lét ta có:
DE//BC ⇒ BC/DE = AB/AD hay x/8 = 28,5/9,5
⇔ x = 8.28,5/9,5 = 456/19 ≈ 31,58

Ta có: A'B'//AB vì cùng vuông góc AA'
Áp dụng hệ quả của định lí Ta – lét ta có:
A'B'//AB ⇒ AB/A'B' = AO/A'O hay x/4,2 = 6/3 ⇔ x = 8,4
Áp dụng định lí Py – ta – go với Δ OAB ta có:
O B 2 = A B 2 + O A 2 ⇒ y = 8 , 4 2 + 6 2 ≈ 10 , 32

+ Hình 14a)
Ta có: MN // EF
⇒ 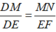 (Hệ quả định lý Ta-let)
(Hệ quả định lý Ta-let)
Mà DM = 9,5 ; DE = DM + ME = 9,5 + 28 = 37,5 ; MN = 8 ; EF = x
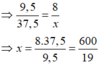
+ Hình 14b)
Ta có: A’B’ ⊥ AA’; AB ⊥ AA’ ⇒ A’B ‘ // AB
⇒ 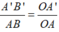 (Hệ quả định lý Ta-let)
(Hệ quả định lý Ta-let)
Mà OA’ = 3 ; OA = 6 ; A’B’ = 4,2 ; AB = x
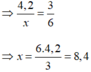
Áp dụng định lý Pytago trong tam giác OAB vuông tại A ta có:
OA2 + AB2 = OB2
Mà OA = 6; AB = x = 8,4 nên
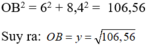

Áp dụng định lý Py-ta-go cho tam giác vuông OA’B’, ta có: O A ’ 2 + A ’ B ’ 2 = O B ' 2
⇔ 2 2 + 4 2 = O B ’ 2 ⇔ O B ' 2 = 20 ⇒ O B ’ = 20
A’B’ ⊥ AA’, AB ⊥ AA’ => A’B’// AB
(Theo định lý từ vuông góc đến song song)
Áp dụng định lý Ta-lét, ta có: O A ' O A = O B ' O B = A ' B ' A B
⇒ 20 x = 2 5 4 y = 2 5 ⇒ x = 5 20 2 = 5 5 y = 4.5 2 = 10
Vậy x = 5 5 , y = 10
Đáp án: D

a) Ta có: \(AC = AK + KC = 3 + 1,5 = 4,5\)
Xét tam giác \(ABC\) có \(HK//BC\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{HK}}{{BC}} = \frac{{AK}}{{AC}} \Rightarrow \frac{x}{6} = \frac{3}{{4,5}}\). Do đó, \(x = \frac{{3.6}}{{4,5}} = 4\).
Vậy \(x = 4\).
b) Ta có: \(MH = MQ + QH = x + 1,8\)
Xét tam giác \(MNH\) có \(PQ//NH\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{PQ}}{{NH}} = \frac{{MQ}}{{MH}} \Rightarrow \frac{{3,8}}{{6,4}} = \frac{x}{{x + 1,8}}\). Do đó, \(6,4x = 3,8.\left( {x + 1,8} \right)\)
\( \Leftrightarrow 6,4x = 3,8x + 6,84\)
\( \Leftrightarrow 6,4x - 3,8x = 6,84\)
\( \Leftrightarrow 2,6x = 6,84\)
\( \Leftrightarrow x = 6,84:2,6\)
\( \Leftrightarrow x = \frac{{171}}{{65}}\).
Vậy \(x = \frac{{171}}{{65}}\).
c) Vì \(\left\{ \begin{array}{l}DE \bot AD\\AB \bot AD\end{array} \right. \Rightarrow DE//AB\) (quan hệ từ vuông góc đến song song).
Xét \(\Delta CDE\) vuông tại \(D\) ta có:
\(E{D^2} + D{C^2} = E{C^2}\) (Định lí Py- ta – go)
\( \Leftrightarrow {8^2} + {6^2} = E{C^2}\)
\( \Leftrightarrow E{C^2} = 100\)
\( \Leftrightarrow EC = 10\)
Xét tam giác \(ABC\) có \(DE//AB\) nên theo hệ quả của định lí Thales ta có:
\(\left\{ \begin{array}{l}\frac{{AC}}{{DC}} = \frac{{AB}}{{ED}} \Rightarrow \frac{5}{6} = \frac{x}{8}\\\frac{{AC}}{{DC}} = \frac{{BC}}{{EC}} \Rightarrow \frac{5}{6} = \frac{y}{{10}}\end{array} \right.\). Do đó, \(\left\{ \begin{array}{l}x = \frac{{5.8}}{6} = \frac{{20}}{3}\\y = \frac{{5.10}}{6} = \frac{{25}}{3}\end{array} \right.\).
Vậy \(x = \frac{{20}}{3};y = \frac{{25}}{3}\).
a)
Xét tam giác ABC có MN//BC
`=>(AM)/MB=(AN)/(NC)` (định lí thales)
`=>(6,5)/x=4/2`
`=>x=3,25`
b)
có QH⊥PH (hình vẽ)
FE⊥PH (hình vẽ)
Suy ra EF//HQ (từ vuông góc đến song song)
Xét tam giác PHQ có EF//HQ (cmt)
`=>(PE)/(PH)=(PF)/(PQ)` (định lí thales)
`=>4/x=5/(5+3,5)`
`=>4/x=5/(8,5)`
`=>x=6,8`