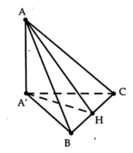
Cho tam giác cân ABC có đường cao AH = \(a\sqrt{3}\), mặt phẳng đáy BC = 3a, BC ⊂(P), A∉(P) . Gọi A' là hình chiếu vuông góc của A lên (P). Tam giác A'BC vuông tại A'. Gọi α là góc giữa (P) và (ABC). Tính α
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
Ta có: B C ⊥ A A ' B C ⊥ A H
![]()
Do đó:
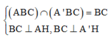
![]()
Mặt khác, tam giác A’BC vuông cân tại A’
nên A ' H = 1 2 B C = 3 a 2
Ta có:
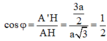
⇒ φ = 60 o

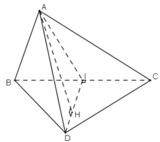
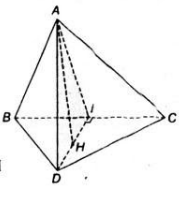
a) Tam giác ABC cân tại A có AI là đường trung tuyến nên đồng thời là đường cao:
AI ⊥ BC
+) Tương tự, tam giác BCD cân tại D có DI là đường trung tuyến nên đồng thời là đường cao:
DI ⊥ BC
+) Ta có: 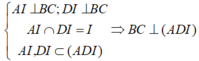
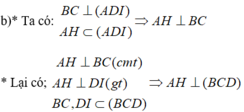

Ta có : A' là h/c của A lên (P) ; BC \(\subset\left(P\right)\) \(\Rightarrow\) \(AA'\perp BC\)
Mà : \(AH\perp BC\) Suy ra : \(BC\perp\left(AA'H\right)\Rightarrow BC\perp A'H\)
Chỉ ra : \(\left(\left(P\right);\left(ABC\right)\right)=\widehat{A'HA}=30^o\)
\(\Delta A'HA\perp\) tại A : \(\dfrac{AH}{A'H}=cos30^o\Rightarrow A'H=\dfrac{\sqrt{3}}{2}.a\sqrt{3}=\dfrac{3a}{2}\)
\(S_{\Delta A'BC}=\dfrac{1}{2}.A'H.BC=\dfrac{1}{2}\dfrac{3a}{2}.3a=\dfrac{9a^2}{4}\)

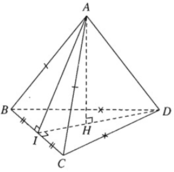
a) Tam giác ABC cân đỉnh A và có I là trung điểm của BC nên AI ⊥ BC. Tương tự tam giác DBC cân đỉnh D và có có I là trung điểm của BC nên DI ⊥ BC. Ta suy ra:
BC ⊥ (AID) nên BC ⊥ AD.
b) Vì BC ⊥ (AID) nên BC ⊥ AH
Mặt khác AH ⊥ ID nên ta suy ra AH vuông góc với mặt phẳng (BCD).

Đáp án A.
Theo giả thiết ta có SO ⊥ (ABC). Gọi D là điểm đối xưng với B qua O
=> ABCD là hình vuông => AB//CD
=> d(AB;SC) = d(AB;(SCD)) = d(E;(SCD)) = 2d(O;(SCD))(Với E, F lần lượt là trung điểm của AB và CD).
Áp dung tính chất tứ diện vuông cho tứ diện OSCD ta có:
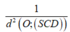
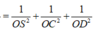
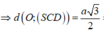
![]()

Đáp án A
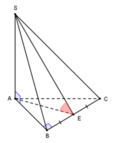
Do SA ⊥ (ABC) tại A nên A là hình chiếu của S lênmặt phẳng (ABC) kéo theo AE là hình chiếu của AE lên mặt phẳng (ABC).
![]()
Áp dụng định lý Py-ta-go trong ∆ S A E vuông tại B, ta có:
![]()
![]()
Trong ∆ S A E vuông tại A SA ⊥ (ABC) nên SA ⊥ AE, ta có:
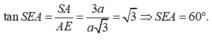

S A B H C
Tam giác ABC vuông cân tại A nên \(BC=2AH=2a\)
Từ đó \(S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}a.2a=a^2\)
Vì \(SA\perp\left(ABC\right);AH\perp BC\) suy ra \(SH\perp BC\)
Do đó : \(\left(\left(SBC\right),\right)\left(ABC\right)=\widehat{SHA}=60^0\)
Suy ra \(SA=AH.\tan60^0=a\sqrt{3}\)
Vậy \(V_{SABC}=\frac{1}{3}SA.S_{ABC}=\frac{1}{3}a\sqrt{3}a^2=\frac{a^3\sqrt{3}}{3}\)