tìm 2 số biết tổng 2 số là 2023 tích hai số là 20232023
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để chứng minh rằng tồn tại một số có dạng 20232023...2023 chia hết cho 19, ta sẽ chứng minh rằng tồn tại một số nguyên n sao cho số nguyên s có dạng sau chia hết cho 19:
s = 20232023...2023 (n chữ số 2023)
Ta có thể biểu diễn s dưới dạng:
s = 2023 x 10⁰ + 2023 x 10¹ + 2023 x 10² + ... + 2023 x 10^(n-1)
= 2023 x (10⁰ + 10¹ + 10² + ... + 10^(n-1))
Để dễ dàng chứng minh, ta sẽ tính tổng sau đây:
10⁰ + 10¹ + 10² + ... + 10^(n-1) = (10⁰ - 1) + (10¹ - 1) + (10² - 1) + ... + (10^(n-1) - 1) + n
= 111...1 (n số 1) + n
= (n + 1) x 111...1 (n số 1)
Do đó:
s = 2023 x (n + 1) x 111...1 (n số 1)
Ta có thể dễ dàng thấy rằng 19 chia hết cho 2023, do đó ta chỉ cần chứng minh rằng (n + 1) x 111...1 (n số 1) chia hết cho 19.
Ta có:
111...1 (n số 1) = (10⁰ + 10¹ + 10² + ... + 10^(n-1)) / 9
= [(10⁰ - 1) + (10¹ - 1) + (10² - 1) + ... + (10^(n-1) - 1)] / 9
= [(n + 1) x 111...1 (n số 1)] / 9
Do đó:
s = 2023 x (n + 1) x [(n + 1) x 111...1 (n số 1)] / 9
= 19 x 1064819 x (n + 1) x [(n + 1) x 111...1 (n số 1)] / (19 x 9)
Như vậy, ta chỉ cần chọn một số nguyên n sao cho (n + 1) x 111...1 (n số 1) chia hết cho 19. Vì 19 là số nguyên tố và không chia hết cho 3, nên ta có thể chọn n = 18, để (n + 1) x 111...1 (n số 1) chia hết cho 19. Vì vậy, tồn tại một số có dạng 20232023...2023 (18 chữ số 2023) chia hết cho 19.

có ngay nhé em.
Nếu số lớn bớt đi 23 thì được số mới gấp 51 lần số bé.
Hiệu số mới với số bé là: 2023 - 23 = 2000
Ta có sơ đồ: 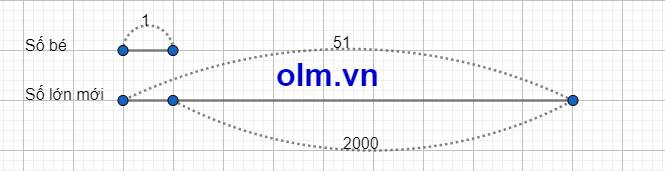
Theo sơ đồ ta có: Số bé là: 2000 : ( 51 - 1) = 40
Số lớn là: 2023 + 40 = 2063
Đáp số: số bé 40
số lớn 2063

các số có tích là 24 là : 3x8;12x2;6x4
mà chỉ có 3x8 là vừa có tích là 24 mà vừa có tổng là 11
suy ra hai số đó là 8 và 3



Cau 1:
vì khi nhân số thứ 1 với 3 và số thứ 2 vowis5 thì được hai tích bàng nhau nên ta có tỉ số giữa số thứ 1 va 2 là 5/3
Ta có sơ đô:
số thứ 1: !------!------!------!------!------!
số thứ 2: !------!------!------!
hiệt số phần bắng nhau là 5-3=2
số thứ nhất là 86/2*5=215
số thứ 2 là 215-86=129

Bài 1. Trong một phép trừ, tổng của số bị trừ, số trừ và hiệu là 100; Tổng của số bị trừ và số trừ là 50. Tìm số bị trừ ?
SBT + ST + H = 100
SBT - ST = H
Vậy:
SBT + ST + SBT - ST = 100
2 SBT = 100
Số bị trừ là:
100 : 2 = 50
Đáp số:
Số bị trừ là 50
Bài 2. Tìm hiệu, tích và thương của hai số, biết tổng hai số đó là 15 và tổng gấp 3 lần số bé.
tổng hai số là 15 và tổng gấp 3 số bé nên số bé = 15:3 =5
Số lớn = tổng - số bé =15-5=10
Hiệu hai số là 10-5=5
tích hai số là 10x5 = 50
thương hai số là 10:5 = 2

Để tìm số tự nhiên a nhỏ nhất thỏa mãn các điều kiện trên, chúng ta có thể thử từng giá trị của a cho đến khi tìm được số a thỏa mãn. Tuy nhiên, để giải quyết bài toán này một cách nhanh chóng, chúng ta có thể sử dụng phương pháp phân tích số học.
Theo yêu cầu của bài toán, ta có:
- A + 1 chia hết cho 2: Điều này có nghĩa là A là số lẻ.
- a chia hết cho tích của hai số nguyên tố liên tiếp: Điều này có nghĩa là a chia hết cho 2 hoặc a chia hết cho 3.
- Tích 2023 x a là số chính phương: Điều này có nghĩa là 2023 x a là một số mà căn bậc hai của nó là một số nguyên.
Với các điều kiện trên, chúng ta có thể thử từng giá trị của a để tìm số a thỏa mãn. Tuy nhiên, để giải quyết bài toán này một cách nhanh chóng, chúng ta có thể sử dụng phương pháp phân tích số học.
Ta có thể phân tích số 2023 thành tích của các thừa số nguyên tố như sau: 2023 = 7 x 17 x 17. Vì vậy, để tích 2023 x a là một số chính phương, ta cần a chia hết cho 7 và 17.
Tiếp theo, ta xét điều kiện a chia hết cho 2 hoặc a chia hết cho 3. Ta thử từng giá trị của a để tìm số a thỏa mãn các điều kiện trên.
Từ các phân tích trên, ta có thể thử các giá trị a như sau:
- a = 7 x 17 = 119: a chia hết cho 7 và 17, và tích 2023 x a = 2023 x 119 = 240737 chính phương.
- a = 2 x 7 x 17 = 238: a chia hết cho 2, 7 và 17, và tích 2023 x a = 2023 x 238 = 482074 chính phương.
Vậy, số tự nhiên a nhỏ nhất thỏa mãn các điều kiện trên là a = 119.
Dài thế bạn
Có đúng ko vậy bài này là đề thi thử mà có 0,5 mà sao khó zậy bạn