Câu 1:Cho hình chóp S. ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong của tam giác SCD
a) Tìm giao điểm N của đường thẳng CD và mặt phẳng (SBM)
b) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC)
c) Tìm giao điểm I của đường thẳng BM và mặt phẳng (SAC)
d) Tìm giao điểm P của SC và mặt pẳng (ABM), từ đó suy ra giao tuyến của hai mặt phẳng (SCD) và (ABM)
Câu 2:
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Trong mặt phẳng đáy vẽ đường thẳng d đi qua A và không song song với các cạnh của hình bình hành, d cắt đoạn BC tại E. Gọi C' là một điểm nằm trên cạnh SC
a) Tìm giao điểm M của CD và mặt phẳng (C'AE)
b) Tìm thiết diện của hình chóp cắt bởi mặt phẳng (C'AE)
Câu 3:
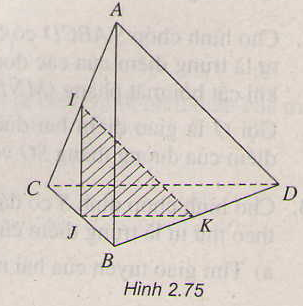
Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của các cạnh AB và CD trên cạnh AD lấy điểm P không trùng với trung điểm của AD
a) Gọi E là giao điểm của đường thẳng MP và đường thẳng BD. Tìm giao tuyến của hai mặt phẳng (PMN) và (BCD)
b) Tìm giao điểm của mặt phẳng (PMN) và BC
Câu 4:
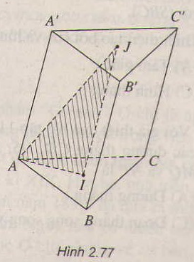
Cho bốn điểm A, B, C và D không đồng phẳng. Gọi I,K lần lượt là trung điểm của hai đoạn thẳng AD và BC
a) Tìm giao tuyến của hai mặt phẳng (IBC) và (KAD)
b) Gọi M và N là hai điểm lần lượt lấy trên hai đoạn thẳng AB và AC. Tìm giao tuyến của hai mặt phẳng (IBC) và (DMN)
Câu 5:
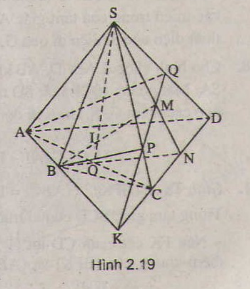
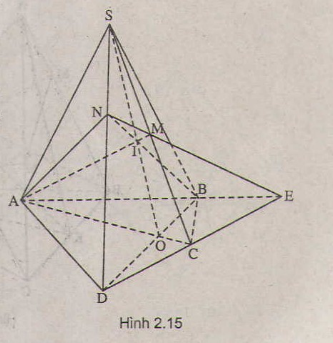
Cho tứ giác ABCD nằm trong mặt phẳng (α) có hai cạnh AB và CD không song song. Gọi S là điểm nằm ngoài mặt phẳng (α) và M là trung điểm đoạn SC.
a) Tìm giao điểm N của đường thẳng SD và mặt phẳng (MAB)
b) Gọi O là giao điểm của AC và BD. Chứng minh rằng ba đường thẳng SO, AM, BN đồng quy
10 giây suy nghĩ cấm tìm trên mạng
hồi sáng tớ đố bài này rùi dễ có trên mạng mà cấm tìm đó
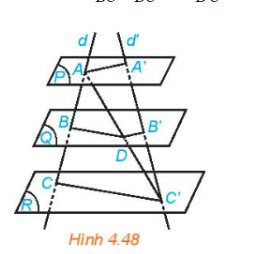


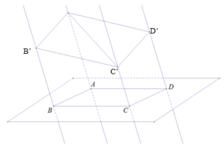
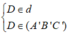

a) Mặt phẳng (Q) và (R) song song với nhau, suy ra giao tuyến của (ACC') với hai mặt phẳng (Q) và (R) song song với nhau. Do đó BD // CC'
Mặt phẳng (Q) và (P) song song với nhau, suy ra giao tuyến của (C'AA') với hai mặt phẳng (Q) và (P) song song với nhau. Do đó B'D // AA'
b) Xét tam giác ACC' ta có BD // CC' suy ra \(\frac{{AD}}{{BC}} = \frac{{AD}}{{DC'}}\)
Xét tam giác C'AA' ta có B'D // AA' suy ra \(ADDC' = A'B'B'C'\)
Do đó, \(\frac{{AB}}{{BC'}} = \frac{{AD}}{{DC'}} = \frac{{A'B'}}{{B'C'}}\)