Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D A' B' C' D' I J
a) Có AA' // DD' và AB//DC nên \(\left(Ax,By\right)\) // \(\left(C_z,D_t\right)\).
b) Do \(\left(Ax,By\right)\) // \(\left(C_z,D_t\right)\) và \(\left(\beta\right)\cap\left(AA'B'B\right)=A'B'\) và \(\left(\beta\right)\cap\left(CC'D'D\right)=C'D'\) nên \(A'B'\) // \(C'D'\).
Chứng minh tương tự B'C'//D'A'.
Do đó tứ giác A'B'C'D' là hình bình hành và J là trung điểm của A'C'.
Suy ra: IJ là đường trung bình của hình thang A'C'CA nên IJ // AA'.
c) Tương tự IJ là đường trung bình của hình thang B'D'DB \(IJ=\dfrac{\left(B'B+DD'\right)}{2}\).
Theo câu b IJ là đường trung bình của hình thang A'C'CA nên \(IJ=\dfrac{\left(AA'+CC'\right)}{2}\).
Suy ra: \(BB'+DD'=AA'+CC'\) hay \(DD'=a+c-b\).

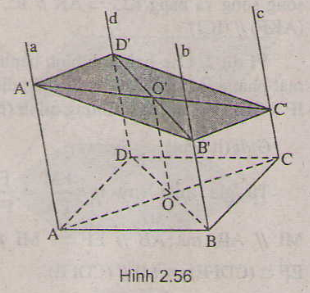
a) Gọi O = AC ∩ BD; O' là trung điểm A'C' thì OO' // AA'
=> OO'// d // b mà O BD
mp (b;d)
=> OO' mp(b;d). Trong mp (b;d) ( mặt phẳng xác định bởi hai đường thẳng song song); d ∩ B'O' = D' là điểm cần tìm
b) Chứng minh mp(a;d) // mp( b;c) , mặt phẳng thứ 3 (A'B'C'D') cắt hai mặt phẳng trên theo hai giao tuyến song song : A'D' // B'C'. Chứng minh tương tự được A'B' // D'C'. Từ đó suy ra A'B'C'D' là hình bình hành

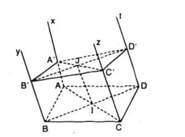
a) Do ABCD là hình bình hành, nên AB // DC
=> AB // (Cz, Dt) (1)
Theo giả thiết Ax // Dt nên Ax // (Cz, Dt) (2)
Từ (1) và (2) suy ra: (Ax, By) // (Cz, Dt)
b) Mặt phẳng β cắt 2 mặt phẳng song song ( Ax, By), (Cz, Dt) theo hai giao tuyến là A’B’và C’D’ nên A’B’// C’D’. (3)
Chứng minh tương tự (Ax, Dt) song song với (By,Cz).Và mặt phẳng β cắt 2 mặt phẳng song song (Ax, Dt), (By, Cz) theo hai giao tuyến là A’D’và B’C’ nên A’D’// B’C’ (4)
Từ (3) và (4) suy ra: tứ giác A’B’C’D’ là hình bình hành.
=> J là trung điểm của A’C’ ( tính chất hình bình hành).
Tứ giác AA’C’C là hình thang vì có: AA’ // CC’ ( giả thiết). Lại có, I và J lần lượt là trung điểm của AC và A’C’ nên IJ là đường trung bình của hình thang
=> IJ// AA’// CC’ ( đpcm).
c) Vì IJ là đường trung bình của hình thang ACC’A’ nên IJ = 1/2(AA’ + CC’)
IJ cũng là đường trung bình của hình thang BDD’B’: IJ = 1/2(BB’ + DD’)
Từ đây suy ra: DD’ + BB’ = AA’ + CC’
=> DD’ = AA’ + CC’ – BB’ = a + c – b

a) \(B{B_1}\)và\(CC'\)song song với nhau
\({B_1}B\)và\(AA'\)song song với nhau
b) Các tỉ số:
\(\frac{{AB}}{{A{B_1}}} = \frac{{BC}}{{{B_1}C'}} = \frac{{CA}}{{C'A'}}\)
\(\frac{{A{B_1}}}{{A'B'}} = \frac{{{B_1}C'}}{{B'C'}} = \frac{{C'A}}{{C'A'}}\)
c) Các tỉ số:\(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{CA}}{{C'A'}}\)
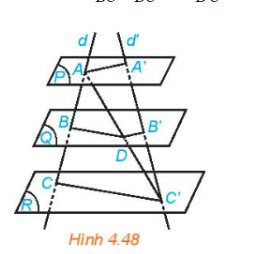






a) Mặt phẳng (Q) và (R) song song với nhau, suy ra giao tuyến của (ACC') với hai mặt phẳng (Q) và (R) song song với nhau. Do đó BD // CC'
Mặt phẳng (Q) và (P) song song với nhau, suy ra giao tuyến của (C'AA') với hai mặt phẳng (Q) và (P) song song với nhau. Do đó B'D // AA'
b) Xét tam giác ACC' ta có BD // CC' suy ra \(\frac{{AD}}{{BC}} = \frac{{AD}}{{DC'}}\)
Xét tam giác C'AA' ta có B'D // AA' suy ra \(ADDC' = A'B'B'C'\)
Do đó, \(\frac{{AB}}{{BC'}} = \frac{{AD}}{{DC'}} = \frac{{A'B'}}{{B'C'}}\)