Cho hình chóp S.ABCD có đáy là hình thang (AB//CD). Hai đường thẳng SD và AB có chéo nhau hay không? Chỉ ra mặt phẳng chứa đường thẳng SD và song song với AB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
23 tháng 8 2023
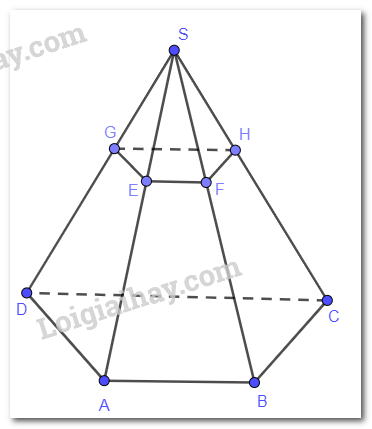
Mặt phẳng (SAD) chứa đường thẳng AD song song với mp(P) nên mặt phẳng (P) cắt (SAD) theo giao tuyến song song với AD. Vẽ EG // AD (G thuộc SD) thì EG là giao tuyến của (P) và (SAD).
Mặt phẳng (SAB) chứa đường thẳng AB song song với mp(P) nên mặt phẳng (P) cắt (SAB) theo giao tuyến song song với AB. Vẽ EF // AB (F thuộc SB) thì EF là giao tuyến của (P) và (SAB).
Ta có AB // CD, EF // AB suy ra CD // EF hay CD // mp(P)
Mặt phẳng (SCD) chứa đường thẳng CD song song với mp(P) nên mặt phẳng (P) cắt (SCD) theo giao tuyến song song với CD. Vẽ GH // CD (H thuộc SC) thì GH là giao tuyến của (P) và (SCD).
FH thuộc (P), FH thuộc (SBC) suy ra FH là giao tuyến của (P) và (SBC).
Tứ giác EFGH có EF // GH (vì cùng song song với CD) suy ra EFGH là hình thang.
CM
15 tháng 2 2019
Cách 1:
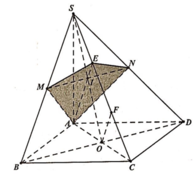
Gọi I là trung điểm của cạnh AD.
∆ A B C vuông cân tại B, ∆ I C D vuông cân tại I và có AB=IC=a nên A C = C D = a 2
Khi đó A C 2 + C D 2 = A D 2 nên ∆ A C D vuông cân tại C.
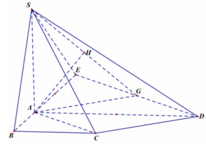
Trong (ABCD), dựng hình vuông ACDE. Trong ∆ S A E , kẻ A H ⊥ S E ( 1 )
Ta có
E D ⊥ S A E D ⊥ A E ⇒ E D ⊥ ( S A E ) ⇒ E D ⊥ A H ( 2 )
Từ (1) và (2) suy ra A H ⊥ ( S D E )
Vì A C / / E D nên
d A C , S D = d A C , S D E = d A ; S D E = A H
Trong ∆ S A E , 1 A H 2 = 1 S A 2 + 1 A E 2
⇔ A H = S A . A E S A 2 = A E 2 ⇔ A H = a . a . 2 a 2 + a 2 ) 2 = 6 a 3
Vậy d A C , S D = 6 a 3
Cách 2:
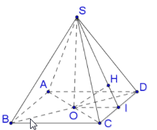
Dễ thấy D C ⊥ ( S A C ) . Trên mặt phẳng (ABCD)
dựng: A G / / C D , D G / / A C , D G ∩ A B = E
Dễ dàng chứng minh được: S.AED là tam diện vuông (1)
Tính được: AE=AD=2a.
Mà A C / / ( S D E )
⇒ d A C , S D = d A C , S D E = d A , S D E = A H
Với AH là đoạn thẳng dựng từ A vuông góc với mặt phẳng (ADE)
Ta có: 1 A H 2 = 1 S A 2 + 1 A E 2 + 1 A D 2
⇒ A H = 6 a 3
Cách 3:
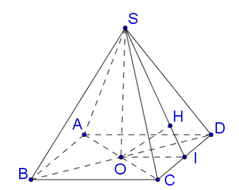
Gắn hệ trục tọa độ Oxyz
Khi đó A ( 0 ; 0 ; 0 ) ; C ( a ; a ; 0 ) ;
D ( 0 ; 2 a ; 0 ) ; S ( 0 ; 0 ; a )
Do đó A C ⇀ = ( a ; a ; 0 ) ; S D ⇀ = ( 0 ; 2 a ; - a ) ; S A ⇀ = ( 0 ; 0 ; - a ) ;
và A C ⇀ ; S D ⇀ = ( - a ; a ; 2 a )
Ta có d A C , S D = A C ⇀ ; S D ⇀ . S A ⇀ A C ; ⇀ S D ⇀
= - a . 0 + a . 0 + 2 a . ( - a ) - a 2 + a 2 + 2 a 2 = 6 a 3
Chọn đáp án C.
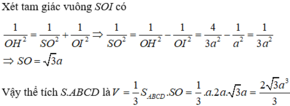
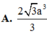
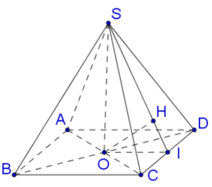
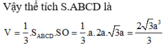
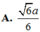
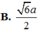
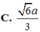
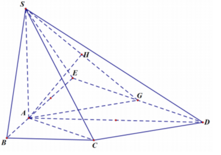
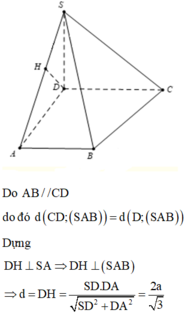
Ta có: SD và AB chéo nhau.
Vì AB và SD chéo nhau nên AB không nằm trong mp(SCD).
Vì AB // CD nên AB // mp(SCD).
Vậy (SCD) là mặt phẳng chứa SD và song song với AB.