Quan sát Hình 6.3, xác định độ lệch pha của hai điểm A và B trên cùng phương truyền sóng vào thời điểm \(t=\dfrac{7T}{4}\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Vì hai điểm gần nhất trên cùng phương truyền sóng dao động lệch pha nhau một góc \(\dfrac{\pi}{2}\)
Khoảng cách giữa hai điểm là 360cm= \(\dfrac{3\lambda}{2}\) nên hai điểm này dao động ngược pha nhau độ lệch pha của chúng là π
b) Sau 0,1s sóng truyền được khoảng cách là 0,1.330 = 33m = \(\dfrac{55\lambda}{4}\)
Độ lệch pha là \(\dfrac{3\pi}{4}\)

Đáp án B
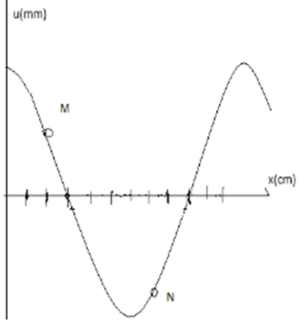
Từ đồ thị, ta gọi mỗi đơn vị khoảng cách trên trục Ox là i. Tọa độ của M là 2i, của N là 7i.
Dễ thấy khoảng cách nửa bước sóng là 6i nên mỗi bước sóng là 12i.
Độ lệch pha giữa hai điểm M, N là:
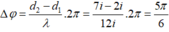

Đáp án B
Từ đồ thị ta xác định được 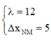 đơn vị độ chia nhỏ nhất của trục Ox.
đơn vị độ chia nhỏ nhất của trục Ox.
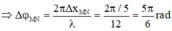

Đáp án B
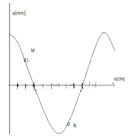
Từ đồ thị, ta gọi mỗi đơn vị khoảng cách trên trục Ox là i. Tọa độ của M là 2i, của N là 7i.
Dễ thấy khoảng cách nửa bước sóng là 6i nên mỗi bước sóng là 12i.
Độ lệch pha giữa hai điểm M, N là:
∆ φ = d 2 - d 1 λ . 2 π = 7 i - 2 i 12 i . 2 π = 5 π 6 .

Đáp án B
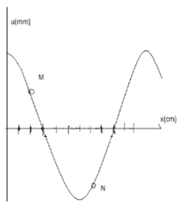
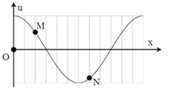
Từ đồ thị, ta gọi mỗi đơn vị khoảng cách trên trục Ox là i. Tọa độ của M là 2i, của N là 7i.
Dễ thấy khoảng cách nửa bước sóng là 6i nên mỗi bước sóng là 12i.
Độ lệch pha giữa hai điểm M, N là:
![]()
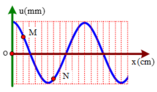
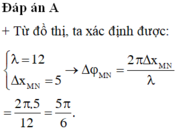
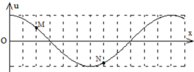
Vì: \(AB=\dfrac{\lambda}{4}\)
Độ lệch pha của hai điểm là:
\(\Delta\varphi=\dfrac{2\pi}{\lambda}AB=\dfrac{2\pi}{\lambda}\cdot\dfrac{\lambda}{4}=\dfrac{2\pi}{4}=\dfrac{\pi}{2}\) rad