Ta có thể dựa vào đồ thị (x – t) của dao động điều hòa để xác định vận tốc và gia tốc của vật được không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tham khảo:
Khi biết phương trình của dao động điều hoà ta có thể sử dụng phương pháp đạo hàm để xác định được vận tốc, gia tốc của vật hoặc có thể xác định các đại lượng đặc trưng của dao động điều hoà và sử dụng các công thức đã biết để tính.Khi biết phương trình của dao động điều hoà ta có thể sử dụng phương pháp đạo hàm để xác định được vận tốc, gia tốc của vật hoặc có thể xác định các đại lượng đặc trưng của dao động điều hoà và sử dụng các công thức đã biết để tính.

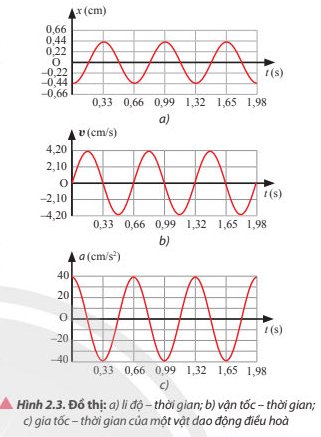
Biên độ dao động: A = 0,44 cm
Tốc độ cực đại: vmax = 4,2 cm/s
Gia tốc cực đại: amax = 40 cm/s2
Chu kì của gia tốc của vật: T = 0,66 s.
Tốc độ góc: \(\omega = \frac{{2\pi }}{T} = \frac{{100}}{{33}}\pi (rad/s)\)
a) Tại thời điểm ban đầu vật đi từ biên âm tiến về VTCB nên pha ban đầu φ0 = π(rad)
Khi đó, phương trình li độ có dạng:
x = Acos(ωt+φ0) = 0,44cos(\(\frac{{100\pi }}{{33}}\)t+π) (cm)
Phương trình vận tốc có dạng:
v = ωAcos(ωt+φ0+\(\frac{\pi }{2}\)) = 4,2cos(\(\frac{{100\pi }}{{33}}\)t+\(\frac{{3\pi }}{2}\)) (cm/s)
Phương trình gia tốc có dạng:
a = −ω2Acos(ωt+φ0) = −40cos(\(\frac{{100\pi }}{{33}}\)t+π) (cm/s2)
b)
Từ đồ thị có thể thấy:
t= 0,33s: x=0,44 cm; v=0 cm/s; a=-40 cm/s2
t= 0,495s: x=0 cm; v=-4,2 cm/s; a=0 cm/s2
t= 0,66s: x=-0,44 cm; v=0 cm/s; a=40 cm/s2
c) Nghiệm lại với các phương trình.
- Tại thời điểm t = 0,5 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).0,5+π) = −0,02 (cm)
v =4,2cos(\(\frac{{100\pi }}{{33}}\).0,5+3π2) = −4,19 (cm/s)
a =−40cos(\(\frac{{100\pi }}{{33}}\).0,5+π) = 1,9 (cm/s2)
- Tại thời điểm t = 0,75 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).0,75+π) = −0,29 (cm)
v = 4,2cos(\(\frac{{100\pi }}{{33}}\).0,75+\(\frac{{3\pi }}{2}\)) = 3,17 (cm/s)
a = −40cos(\(\frac{{100\pi }}{{33}}\).0,75+π) = 26,2 (cm/s2)
- Tại thời điểm t = 1 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).1+π) = 0,438 (cm)
v = 4,2cos(\(\frac{{100\pi }}{{33}}\).1+3π2) = −0,4 (cm/s)
a = −40cos(\(\frac{{100\pi }}{{33}}\).1+π) = −39,8 (cm/s2)

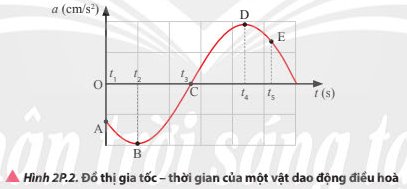
Vị trí A có gia tốc a1=−ω2.A
Vị trí B có gia tốc a2=0 nên vật ở vị trí cân bằng có vận tốc bằng v=ωA
Vị trí C có gia tốc a3=−ω2.A>0 nên vật ở vị trí biên âm có vận tốc bằng 0

Đáp án D
Vì hệ thức liên hệ giữa gia tốc và vận tốc là:
v 2 A 2 ω 2 + a 2 A 2 ω 4 = 1 , đây là đồ thị của Elip.

Đáp án D
Vì hệ thức liên hệ giữa gia tốc và vận tốc là:
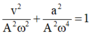
=> đây là đồ thị của Elip.

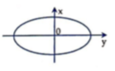
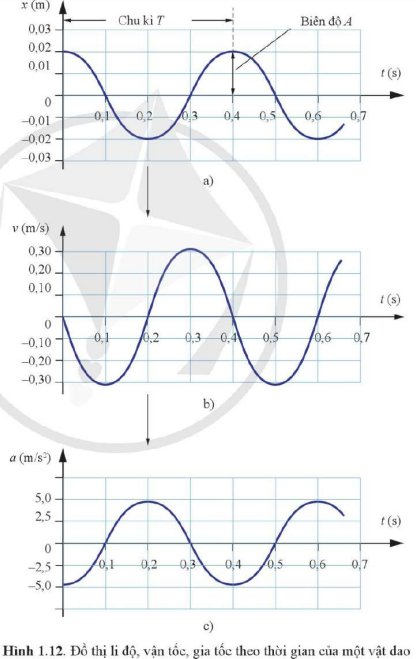
`***` Hình `a`:
`a, \omega =[2\pi]/[0,4]=5\pi (rad//s)`
`b, A=0,03(m)=3(cm)`
`c, v_[max]=5\pi .3=15 \pi(cm//s)`
`d, a_[max]=(5\pi)^2 .3=75 \pi^2 (cm//s^2)`
`***` Hình `b`:
`a, \omega =[2\pi]/[0,4]= 5 \pi(rad//s)`
`b, A=[0,3]/[5\pi]=3/[50 \pi] (m)=6/[\pi] (cm)`
`c, v_[max]=30 (cm//s)`
`d, a_[max]=30.5\pi=150\pi (cm//s^2)`
`***` Hình `c`:
`a, \omega=[2\pi]/[0,4]=5\pi (rad//s)`
`b, A=5/[(5\pi)^2]=1/[5\pi^2] (m)`
`c, v_[max]=5\pi . 1/[5\pi^2]=1/[\pi] (m//s)`
`d, a_[max]=5(m//s^2)`

Với định luật bảo toàn cơ năng ta có thể tìm được li độ và vận tốc vật trong dao động điều hòa:
\(W_đ=W_t=W\)
\(\Leftrightarrow\dfrac{1}{2}mv^2=\dfrac{1}{2}m\omega^2x^2=\dfrac{1}{2}m\omega^2A^2\)
Vì vận tốc tức thời được tính bằng công thức:
\(v=\dfrac{\Delta x}{\Delta t}\)
Và gia tốc tính bằng công thức:
\(a=\dfrac{\Delta x}{\Delta v}\)