phần c) ạ.Dạng bài giải pt vô tỉ bằng pp đặt ẩn phụ.
p
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
30 tháng 8 2023
Lời giải:
Đặt $(x-3)^2=a$. Khi đó pt đã cho tương đương với:
$(x^2-6x+9-9)^2+13(x-3)^2-77=0$
$\Leftrightarrow [(x-3)^2-9]^2+13(x-3)^2-77=0$
$\Leftrightarrow (a-9)^2+13a-77=0$
$\Leftrightarrow a^2-5a+4=0$
$\Leftrightarrow (a-1)(a-4)=0$
$\Leftrightarroe a=1$ hoặc $a=4$
Đến đây thì đơn giản rồi.
MA
0
VV
1
VD
17 tháng 3 2022
ĐKXĐ:\(\left\{{}\begin{matrix}x\ne3\\y\ne1\end{matrix}\right.\)
Đặt `(x)/(x-3)` = a, `(y)/(y-1)` = b
\(\text{Hệ}\Leftrightarrow\left\{{}\begin{matrix}a+3b=5\\4a-b=7\end{matrix}\right.\\ \Leftrightarrow...\\ \Leftrightarrow\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{x-3}=2\\\dfrac{y}{y-1}=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=2x-6\\y=y-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=6\\-1=0\left(vô.lí\right)\end{matrix}\right.\)
Vậy hpt vô nghiệm
7 tháng 4 2022
Đặt \(\sqrt{x^2+x+1}=a\)
Pt trở thành \(3a=a^2+2\)
=>(a-1)(a-2)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+x+1=1\\x^2+x+1=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2+x=0\\\left(x+\dfrac{1}{2}\right)^2=\dfrac{13}{4}\end{matrix}\right.\)
\(\Leftrightarrow x\in\left\{0;-1;\dfrac{\sqrt{13}-1}{2};\dfrac{-\sqrt{13}-1}{2}\right\}\)
7 tháng 4 2022
b: \(\Leftrightarrow\left(x^2+3x-1\right)^2+4\left(x^2+3x-1\right)-2\left(x^2+3x-1\right)-8=0\)
\(\Leftrightarrow\left(x^2+3x-1\right)\left(x^2+3x-1+4\right)-2\left(x^2+3x-1+4\right)=0\)
\(\Leftrightarrow x^2+3x-3=0\)
\(\Delta=3^2-4\cdot1\cdot\left(-3\right)=9+12=21>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-3-\sqrt{21}}{2}\\x_2=\dfrac{-3+\sqrt{21}}{2}\end{matrix}\right.\)
d: \(\Leftrightarrow\left(x^2-3x\right)^2+6\left(x^2-3x\right)+8=3\)
\(\Leftrightarrow\left(x^2-3x\right)^2+5\left(x^2-3x\right)+\left(x^2-3x\right)+5=0\)
\(\Leftrightarrow x^2-3x+1=0\)
\(\Delta=\left(-3\right)^2-4\cdot1\cdot1=5>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{3-\sqrt{5}}{2}\\x_2=\dfrac{3+\sqrt{5}}{2}\end{matrix}\right.\)
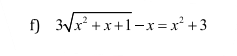
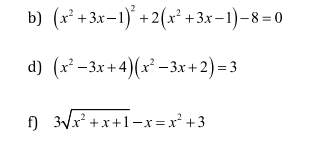
Lời giải:
Đặt $\sqrt[3]{2x+1}=a; \sqrt[3]{x}=b$ thì ta có:
$a+b=1$ và $a^3-2b^3=1$
$\Rightarrow a^3-2b^3=(a+b)^3$
$\Leftrightarrow a^3-2b^3=a^3+3a^2b+3ab^2+b^3$
$\Leftrightarrow 3a^2b+3ab^2+3b^3=0$
$\Leftrightarrow b(a^2+ab+b^2)=0$
$\Leftrightarrow b=0$ hoặc $a^2+ab+b^2=0$
Nếu $b=0\Leftrightarrow \sqrt[3]{x}=0\Leftrightarrow x=0$ (thử lại thấy tm)
Nếu $a^2+ab+b^2=0$
$\Leftrightarrow (a+\frac{b}{2})^2+\frac{3}{4}b^2=0$
$\Rightarrow a+\frac{b}{2}=b=0$
$\Rightarrow a=b=0$
$\Leftrightarrow \sqrt[3]{2x+1}=\sqrt[3]{x}=0$
$\Leftrightarrow x=\frac{-1}{2}=0$ (vô lý)
Vậy $x=0$