nêu tính chất của số 1 và số 0 trong phép nhân và phép chia
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số nào nhân chia với 1 thì cũng bằng chính nó.
Số nào nhân với 0 thì cũng bằng 0.
Không co phép chia cho 0.
Số nào nhân với 1 hoặc chia cho 1 thì bằng chính nó
Số nào nhân với 0 thì có kết quả bằng 0
Không có phép chia cho 0


A ) Tập hợp a là tập hợp con của b khi tất cả các phần tử có trong a phải có trong b
B ) Tập hợp a = tập hợp b khi cả hai tập hợp đều có số phần tử như nhau ! ( mình ko chắc )
c ) Phép cộng và phép nhân có những tính chất là giao hoán kết hợp , tính chất phân phối giữ phép nhân và phép cộng .
GIÚP ĐƯỢC THÌ GIÚP THÔI CHỨ MÌNH KO CHẮC !

Ta đã biết tính chất kết hợp của phép nhân là:
(a.b).c = a.(b.c)
Từ đó ta có:
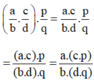
(áp dụng tính chất kết hợp của số nguyên cho cả tử và mẫu)
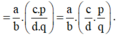
Vậy 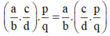 (tính chất kết hợp của phép nhân phân số)
(tính chất kết hợp của phép nhân phân số)

1 .
| Tính chất | Phép cộng | Phép nhân |
| Giao hoán | a + b = b +a | a . b = b . a |
| Kết hợp | ( a + b ) + c = a + (b + c) | (a . b) . c = a . ( b . c ) |
| Phân phối của phép nhân với phép cộng | ( a + b ) . c = a . b + b . c |
2 . Luỹ thừa bậc n của a là tích của n thừa số bằng nhau , mỗi thừa số bằng a
3 . am . an = am + n
am : an = am - n
4 . Ta nói số tự nhiên a chia hết cho số tự nhiên b khi có số tự nhiên q sao cho : a = bq
5 . Đối với biểu thức không có ngoặc :
Ta thực hiện phép tính nâng lên luỹ thừa , rồi đến nhân và chia , cuối cùng là cộng và trừ
Tổng quát : Luỹ thừa -> Nhân và chia -> Cộng và trừ
Đối với biểu thức có dấu ngoặc
Từ ngoặc tròn đến ngoặc vuông rồi cuối cùng đến ngoặc vuông
Tổng quát : ( ) -> [ ] -> { }
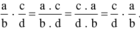
số nào nhân chia với 1 thì cũng bằng chính nó
số nào nhân với 0 thì cũng bằng 0
ko co phép chia cho 0
k nha
Số nào nhân, chia cho 1 thì bằng chính số đó.
Số nào nhân với 0 thì bằng 0
Không có phép chia cho 0