Đặt nhân tử chung rồi giản ước
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ab - bd - be + ce + cd + ae = (ab - be) - (bd - cd) + (ce + ae)
= b(a - e) - d(b - c) + e(c + a)
Xem lại đề nhé, hơi căng :))

a) 5x + 10 = 5(x + 2)
25x2 + 50x = 25x(x + 2)
⇒ Nhân tử chung của chúng là: 5(x + 2)
b)
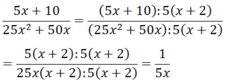

h: =3(x^2+3x-10)
=3(x^2+5x-2x-10)
=3[x(x+5)-2(x+5)]
=3(x+5)(x-2)
e: =x^2-2x-4x+8
=x(x-2)-4(x-2)
=(x-2)(x-4)
h: =x^2-3x-4x+12
=x(x-3)-4(x-3)
=(x-3)(x-4)
Lời giải:
b. $3x^2+9x-30=3(x^2+3x-10)$
$=3[(x^2-2x)+(5x-10)]=3[x(x-2)+5(x-2)]=3(x-2)(x+5)$
e. $x^2-6x+8=(x^2-2x)-(4x-8)=x(x-2)-4(x-2)=(x-4)(x-2)$
h. $x^2-7x+12=(x^2-3x)-(4x-12)=x(x-3)-4(x-3)=(x-3)(x-4)$


\(=\left(3x+15\right)^2-\left(x-7\right)^2\\ =\left(3x+15-x+7\right)\left(3x+15+x-7\right)\\ =\left(2x+22\right)\left(4x+8\right)\\ =2\left(x+11\right)4\left(x+2\right)\\ =8\left(x+11\right)\left(x+2\right)\)

\(=\left(x^2+y^2-5\right)^2-\left[2\left(xy+2\right)\right]^2\\ =\left(x^2+y^2-5-2xy-4\right)\left(x^2+y^2-5+2xy+4\right)\\ =\left[\left(x-y\right)^2-9\right]\left[\left(x+y\right)^2-1\right]\\ =\left(x-y-3\right)\left(x-y+3\right)\left(x+y-1\right)\left(x+y+1\right)\)
\(=\left(x^2+y^2-5\right)^2-4\left(xy+2\right)^2\)
\(=\left(x^2+y^2-5\right)^2-\left(2xy+4\right)^2\)
\(=\left(x^2+y^2-5-2xy-4\right)\left(x^2+y^2-5+2xy+4\right)\)
\(=\left[\left(x-y\right)^2-9\right]\left[\left(x-y\right)^2-1\right]\)
\(=\left(x-y-3\right)\left(x-y+3\right)\left(x-y-1\right)\left(x-y+1\right)\)

= \(-\left(x^2+4xy+4y^2\right)\)
= \(-\left(x+2y\right)^2\)
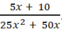
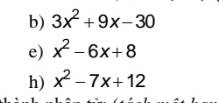
\(=\dfrac{\sqrt{3}\left(\sqrt{5}-1\right)}{\sqrt{5}-1}-\sqrt{6}-3-\sqrt{6}\)
=căn 3-2căn 6-3