Cho hàm số: \(y=x+cos^2x\). Xác định tính đơn điệu của hàm số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Ta có y ' = f ' x − 2 dựa trên đồ thị ta thấy x ∈ 1 ; + ∞ ⇒ f ' x > 2 ⇒ f ' x − 2 > 0 ⇒ y đồng biến

TXĐ: D=(\(-\infty;2\)]
\(y'=1+2.\dfrac{-1}{2\sqrt{2-x}}\)\(=1-\dfrac{1}{\sqrt{2-x}}\)
Ta có bảng biến thiên sau:
| x | \(-\infty\) 1 2 |
| y' | + 0 - || |
Vậy hàm số đồng biến trên khoảng \(\left(-\infty;1\right)\) và nghịch biến trên khoảng \(\left(1;2\right)\)

ĐKXĐ:
a. \(\left\{{}\begin{matrix}x-1\ge0\\x-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge1\\x\ne3\end{matrix}\right.\) \(\Rightarrow D=[1;+\infty)\backslash\left\{3\right\}\)
b. \(D=R\)
c. \(x+3>0\Rightarrow x>-3\Rightarrow D=\left(-3;+\infty\right)\)
d. \(\left|x-2\right|\ge0\Rightarrow x\in R\Rightarrow D=R\)

Câu 2:
a) Để đồ thị hàm số \(y=\left(m+1\right)x^2\) đi qua điểm A(1;2) thì
Thay x=1 và y=2 vào hàm số \(y=\left(m+1\right)x^2\), ta được:
m+1=2
hay m=1
Vậy: m=1

a) + Hàm số y = cos x có chu kì 2π.
Do đó: cos 2.(x + kπ) = cos (2x + k2π) = cos 2x.
⇒ Hàm số y = cos 2x cũng tuần hoàn với chu kì π.
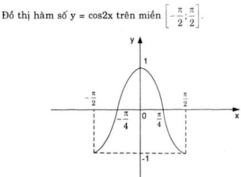
Từ đó suy ra
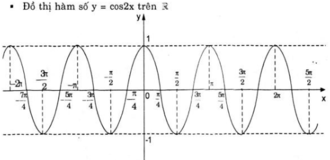
b. y = f(x) = cos 2x
⇒ y’ = f’(x) = (cos 2x)’ = -(2x)’.sin 2x = -2.sin 2x.
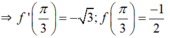
⇒ Phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π/3 là:
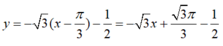
c. Ta có: 1 – cos 2x = 2.sin2x ≥ 0.
Và 1 + cos22x > 0; ∀ x
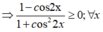
⇒ 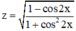 luôn xác định với mọi x ∈ R.
luôn xác định với mọi x ∈ R.

Đáp án B
+ Xét hàm y = f(x) = cos (x + π)
TXĐ: D = R
Với mọi x ∈ D, ta có: -x ∈ D và f(-x) = cos (-x + π) = -cos x = cos (x + π) = f(x)
Do đó y = cos (x + π) là hàm số chẵn .
+ Xét hàm y = g(x) = tan2016x
TXĐ: D = R\{π/2 + kπ, k ∈ Z}
Với mọi x ∈ D, ta có: -x ∈ D và g(-x) = tan2016(-x) = (-tan x)2016 = tan2016x = g(x)
Do đó: y = tan2016x là hàm chẵn trên tập xác định của nó.
+Xét hàm y = cot2x
f(-x) = cot(-2x) = - cot 2x = -f(x) nên đây là hàm số lẻ.
+ Xét hàm số y = 1-sinx
f(-x) = 1- sin(-x) = 1+ sin x
Nên hàm số không chẵn không lẻ


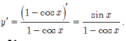
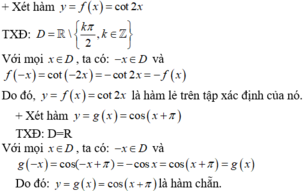
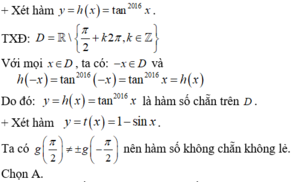
\(y'=1-2.cosx.sinx=1-sin2x\le0,\forall x\)
Vậy hàm số nghịch biến trên R
Đạo hàm của hàm số y = x +` cos^2(x)`
Đạo hàm của x là 1
Đạo hàm của `cos^2(x) là -2sin(x)cos(x)` (sử dụng công thức đạo hàm của `cos^2(x)`).
Vậy, đạo hàm của hàm số y = x + `cos^2(x)` là `dy/dx = 1 - 2sin(x)cos(x).`
Khi `sin(x)cos(x) < 1/2`, tức là x thuộc khoảng `(0, π)` hoặc `(2π, 3π)`, ta có `1 - 2sin(x)cos(x) > 0.`
Khi `sin(x)cos(x) > 1/2`, tức là x thuộc khoảng `(π, 2π)`, ta có `1 - 2sin(x)cos(x) < 0.`
Vậy, trên các khoảng `(0, π)` và `(2π, 3π)`, đạo hàm là dương, và trên khoảng `(π, 2π)`, đạo hàm là âm.
Kết luận: hàm số y = x + `cos^2(x)` tăng trên các khoảng `(0, π)` và `(2π, 3π)`, và giảm trên khoảng `(π, 2π).`
Vậy, tính đơn điệu của hàm số y = x + `cos^2(x)` là tăng trên các khoảng `(0, π)` và `(2π, 3π)`, và giảm trên khoảng `(π, 2π).`