Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)



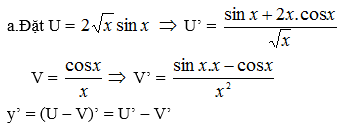
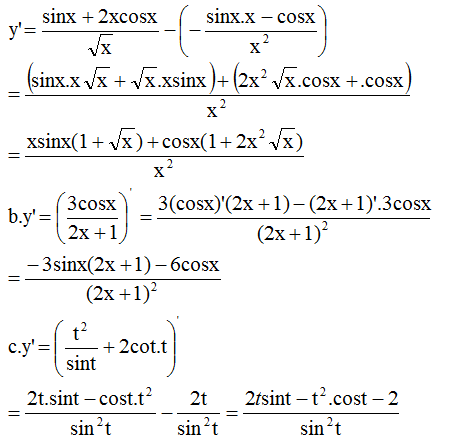
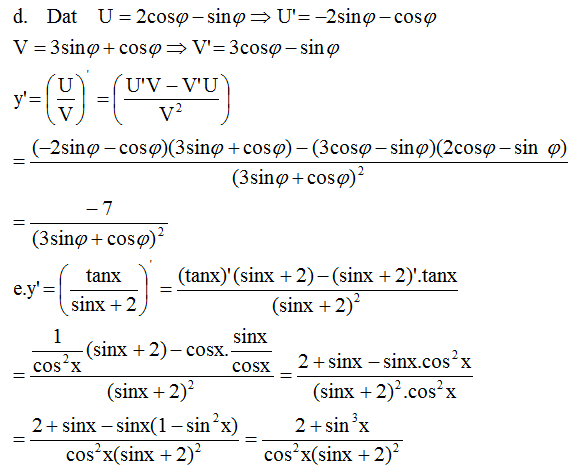
Đáp án B
+ Xét hàm y = f(x) = cos (x + π)
TXĐ: D = R
Với mọi x ∈ D, ta có: -x ∈ D và f(-x) = cos (-x + π) = -cos x = cos (x + π) = f(x)
Do đó y = cos (x + π) là hàm số chẵn .
+ Xét hàm y = g(x) = tan2016x
TXĐ: D = R\{π/2 + kπ, k ∈ Z}
Với mọi x ∈ D, ta có: -x ∈ D và g(-x) = tan2016(-x) = (-tan x)2016 = tan2016x = g(x)
Do đó: y = tan2016x là hàm chẵn trên tập xác định của nó.
+Xét hàm y = cot2x
f(-x) = cot(-2x) = - cot 2x = -f(x) nên đây là hàm số lẻ.
+ Xét hàm số y = 1-sinx
f(-x) = 1- sin(-x) = 1+ sin x
Nên hàm số không chẵn không lẻ