Câu 5: Cho hình chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông tâm O cạnh bằng a, góc giữa cạnh bên và mặt đáy 1 góc 60°. Gọi IE lần lượt là là trung điểm của cạnh BC,CD a)Chứng minh: AC vuông góc (SBD) ; BD vuông góc SA b)Chứng minh: (SBC) vuông góc (SOI) c)Tính góc giữa mặt bên và mặt đáy. d)góc giữa OE và mặt (SCD) e)Tính khoảng cách giữa SI và AB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi H là trung điểm của AD. Do tam giác SAD là tam giác đều nên SH vuông góc với AD
Do mặt phẳng (SAD) vuông góc với mặt phẳng (ABCD) nên SH vuông góc với BP(1)
Xét hình vuông ABCD ta có :
\(\Delta CDH=\Delta BCP\Rightarrow CH\perp BP\) (2)
Từ (1) và (2) ta suy ra \(BP\perp\left(SHC\right)\)
Vì \(\begin{cases}MN||SC\\AN||CH\end{cases}\) \(\Rightarrow\left(AMN\right)||\left(SHC\right)\)
\(\Rightarrow BP\perp\left(AMN\right)\Rightarrow BP\perp AM\)
Kẻ vuông góc với mặt phẳng (ABCD), K thuộc vào mặt phẳng (ABCD), ta có :
\(V_{CMNP}=\frac{1}{3}MK.S_{CNP}\)
Vì \(MK=\frac{1}{2}SH=\frac{a\sqrt{3}}{4};S_{CNP}=\frac{1}{2}CN.CP=\frac{a^2}{8}\)
\(\Rightarrow V_{CMNP}=\frac{\sqrt{3}a^2}{96}\)

Chọn B
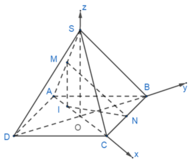
Gọi I là hình chiếu của M lên (ABCD), suy ra I là trung điểm của AO.
Khi đó
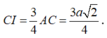
Xét tam giác CNI có
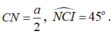
Áp dụng định lý cosin ta có:
![]()

Xét tam giác MIN vuông tại I nên
![]()
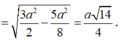
Mà MI//SO
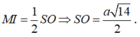
Chọn hệ trục tọa độ như hình vẽ. Ta có:
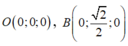
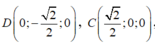
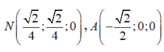
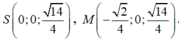
Khi đó
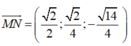
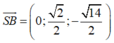
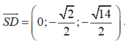
Vectơ pháp tuyến mặt phẳng (SBD)
![]()
Suy ra
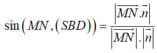
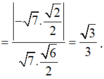

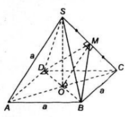
a) Theo giả thiết, S.ABCD là hình chóp đều và đáy ABCD là hình vuông nên SO ⊥ (ABCD) ( tính chất hình chóp đều)
Đáy ABCD là hình vuông cạnh a nên
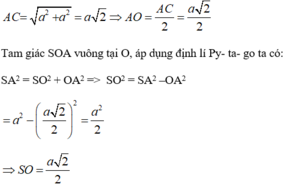

=> Góc giữa hai mặt phẳng (MBD) và (ABCD) là 45 o

Chọn đáp án C.
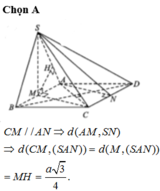
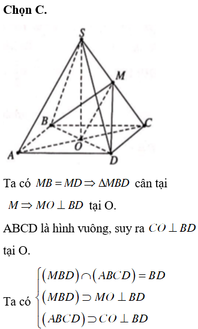
Gọi O là tâm của hình vuông ABCD thì B D ⊥ S A O

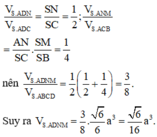


Do S.ABCD là chóp đều \(\Rightarrow BD\perp\left(SAC\right)\)
Mà BD là giao tuyến (MBD) và (ABCD)
\(\Rightarrow\widehat{MOC}\) là góc giữa (MBD) và (ABCD)
\(OC=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\) ; \(MC=OM=\dfrac{1}{2}SC=\dfrac{a}{2}\)
Áp dụng định lý hàm cosin:
\(cos\widehat{MOC}=\dfrac{OM^2+OC^2-CM^2}{2OM.OC}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{MOC}=45^0\)
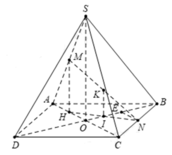



a: AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SBD)
=>SB vuông góc AC
mà AC vuông góc BD
nên AC vuông góc (SBD)
BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=>BD vuông góc SA
b: Xét ΔACB có CO/CA=CI/CB
nên OI//AB
=>OI vuông góc BC
BC vuông góc OI
BC vuông góc SO
=>BC vuông góc (SOI)
=>(SBC) vuông góc (SOI)