P=3/(căn x+1) c) tìm các giá trị của x để 1/P=4/5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 6 2021
`A=sqrt{x-2}+sqrt{6-x}(2<=x<=6)`
Áp dụng BĐT `sqrtA+sqrtB>=sqrt{A+B}`
`=>A>=sqrt{x-2+6-x}=2`
Dấu "=" `<=>x=2` hoặc `x=6`
Áp dụng BĐT bunhia
`=>A<=sqrt{2(x-2+6-x)}=2sqrt2`
Dấu "=" `<=>x=4`
`C=sqrt{1+x}+sqrt{8-x}(-1<=x<=8)`
Áp dụng BĐT `sqrtA+sqrtB>=sqrt{A+B}`
`=>A>=sqrt{1+x+8-x}=3`
Dấu "=" `<=>x=-1` hoặc `x=8`
Áp dụng BĐT bunhia
`=>A<=sqrt{2(1+x+8-x)}=3sqrt2`
Dấu "=" `<=>x=7/2`
5 tháng 6 2021
`D=2sqrt{x+5}+sqrt{1-2x}(-5<=x<=1/2)`
`=sqrt{4x+20}+sqrt{1-2x}`
Áp dụng BĐT `sqrtA+sqrtB>=sqrt{A+B}`
`=>D>=sqrt{4x+20+1-2x}=sqrt{2x+21}`
Mà `x>=-5`
`=>D>=sqrt{-10+21}=sqrt{11}`
Dấu "=" `<=>x=-5`
15 tháng 6 2021
a, \(A=\left(\frac{1}{1-\sqrt{x}}+\frac{1}{1+\sqrt{x}}\right):\left(\frac{1}{1-\sqrt{x}}-\frac{1}{1+\sqrt{x}}\right)+\frac{1}{1-\sqrt{x}}\)ĐK : \(x>0;x\ne1\)
\(=\left(\frac{1+\sqrt{x}+1-\sqrt{x}}{1-x}\right):\left(\frac{1+\sqrt{x}-1+\sqrt{x}}{1-x}\right)+\frac{1}{1-\sqrt{x}}\)
\(=\frac{2}{1-x}.\frac{1-x}{2\sqrt{x}}+\frac{1}{1-\sqrt{x}}=\frac{1}{\sqrt{x}}+\frac{1}{1-\sqrt{x}}=\frac{1-\sqrt{x}+\sqrt{x}}{-x+\sqrt{x}}=\frac{1}{\sqrt{x}-x}\)
b, Ta có : \(x=7+4\sqrt{3}=7+2.2\sqrt{3}=\left(\sqrt{4}+\sqrt{3}\right)^2\)
\(A=\frac{1}{\sqrt{4}+\sqrt{3}-7+4\sqrt{3}}\)
ND
1
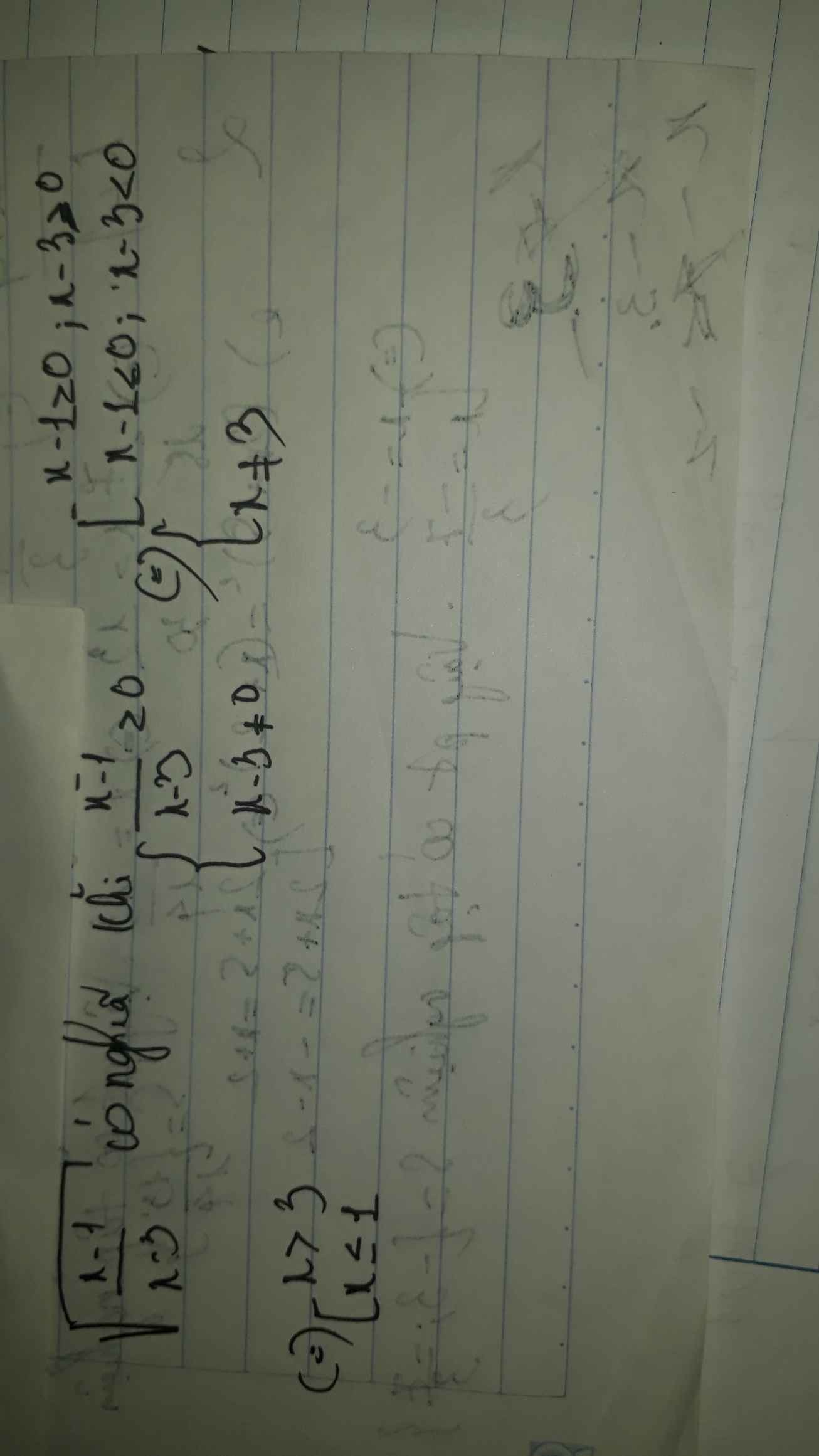
c) Ta có: \(\dfrac{1}{P}=\dfrac{4}{5}\)
\(\Rightarrow1:\left(\dfrac{3}{\sqrt{x}+1}\right)=\dfrac{4}{5}\)
\(\Leftrightarrow\dfrac{3}{\sqrt{x}+1}=\dfrac{5}{4}\)
\(\Leftrightarrow5\left(\sqrt{x}+1\right)=12\)
\(\Leftrightarrow\sqrt{x}-1=\dfrac{12}{5}\)
\(\Leftrightarrow\sqrt{x}=\dfrac{12}{5}+1\)
\(\Leftrightarrow\sqrt{x}=\dfrac{17}{5}\)
\(\Leftrightarrow x=\left(\dfrac{17}{5}\right)^2=\dfrac{289}{25}\)
Sửa đề : (xem lại)
`c)1/P=4/3`
`=>P=3/4`
`<=>3/(\sqrtx+1)=3/4`
`=>\sqrtx+1=4`
`=>\sqrtx=3`
`=>x=9(t/m)`
Vậy với `x=9` thì `1/P=4/3`