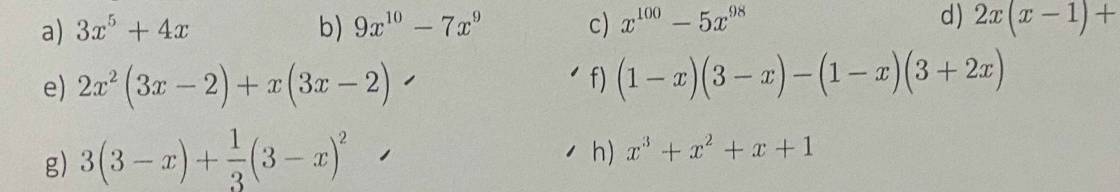
tìm nghiệm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b, Để phương trình có 2 nghiệm \(\Delta\ge0\)
hay \(\left(2m+8\right)^2-4.m^2=4m^2+32m+64-4m^2=32m+64\ge0\)
\(\Leftrightarrow32m\ge64\Leftrightarrow m\ge2\)
Theo Vi et ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+8\\x_1x_2=\dfrac{c}{a}=m^2\end{matrix}\right.\)
mà \(\left(x_1+x_2\right)^2=4m^2+32m+64\Rightarrow x_1^2+x_2^2=4m^2+32m+64-2x_1x_2\)
\(=4m^2+32m+64-2m^2=2m^2+32m+64\)
Lại có : \(x_1^2+x_2^2=-2\)hay \(2m^2+32m+66=0\Leftrightarrow m=-8+\sqrt{31}\left(ktm\right);m=-8-\sqrt{31}\left(ktm\right)\)
a) Thay m=8 vào phương trình, ta được:
\(x^2-2\cdot\left(8+4\right)x+8^2=0\)
\(\Leftrightarrow x^2-24x+64=0\)
\(\text{Δ}=\left(-24\right)^2-4\cdot1\cdot64=576-256=320\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{24+8\sqrt{5}}{2}=12+4\sqrt{5}\\x_2=\dfrac{24-8\sqrt{5}}{2}=12-4\sqrt{5}\end{matrix}\right.\)
Vậy: Khi m=8 thì phương trình có hai nghiệm phân biệt là \(x_1=12+4\sqrt{5};x_2=12-4\sqrt{5}\)

a: Δ=(4m+3)^2-4*2*(2m^2-1)
=16m^2+24m+9-16m^2+8
=24m+17
Để phương trình có hai nghiệm phân biệt thì 24m+17>0
=>m>-17/24
b: Để phương trìh có nghiệm kép thì 24m+17=0
=>m=-17/24
c: Để phương trình vô nghiệm thì 24m+17<0
=>m<-17/24

a) Thay m=3 vào pt ta được:
\(9x+6=4x+9\Leftrightarrow x=\dfrac{3}{5}\)
Vậy...
b) Thay x=-1,5 vào pt ta được:
\(m^2\left(-1,5\right)+6=4.\left(-1,5\right)+3m\)
\(\Leftrightarrow\dfrac{-3}{2}m^2-3m+12=0\)\(\Leftrightarrow\left[{}\begin{matrix}m=2\\m=-4\end{matrix}\right.\)
Vậy...
c)Pt \(\Leftrightarrow x\left(m^2-4\right)=3m-6\)
Để pt vô nghiệm \(\Leftrightarrow\left\{{}\begin{matrix}3m-6\ne0\\m^2-4=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\m=\pm2\end{matrix}\right.\)\(\Rightarrow m=-2\)
Để pt có vô số nghiệm \(\Leftrightarrow\left\{{}\begin{matrix}3m-6=0\\m^2-4=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m=2\\m=\pm2\end{matrix}\right.\)\(\Rightarrow m=2\)
d)Để pt có nghiệm \(\Leftrightarrow m^2-4\ne0\Leftrightarrow m\ne\pm2\)
\(\Rightarrow x=\dfrac{3m-6}{m^2-4}=\dfrac{3\left(m-2\right)}{\left(m-2\right)\left(m+2\right)}=\dfrac{3}{m+2}\)
Để \(x\in Z\Leftrightarrow\dfrac{3}{m+2}\in Z\)
Vì \(m\in Z\Leftrightarrow m+2\in Z\).Để \(\dfrac{3}{m+2}\in Z\Leftrightarrow m+2\inƯ\left(3\right)=\left\{-1;-3;1;3\right\}\)
\(\Leftrightarrow m=\left\{-3;-5;-1;1\right\}\) (tm)
Vậy...


Ý bạn ấy là \(x_1^2\)nhưng bạn ấy chưa biết chỗ để đánh chỉ số dưới. Bạn nhấn vào cái biểu tượng x2 ở chỗ khung điều chỉnh thì con trỏ hạ xuống để bạn gõ chỉ số dưới. Xong rồi thì nhấn vào biểu tượng đó lần nữa.

a) Thay \(m=1\) vào phương trình, ta được:
\(x^2+12x-4=0\) \(\Rightarrow\left[{}\begin{matrix}x=-6+2\sqrt{10}\\x=-6-2\sqrt{10}\end{matrix}\right.\)
Vậy ...
b)
+) Với \(m=0\) \(\Rightarrow12x-4=0\) \(\Leftrightarrow x=\dfrac{1}{3}\)
+) Với \(m\ne0\), ta có: \(\Delta'=36+4m\)
Để phương trình có 2 nghiệm phân biệt \(\Leftrightarrow\Delta'>0\) \(\Leftrightarrow m>-9\)
Vậy \(\left\{{}\begin{matrix}m\ne0\\m>-9\end{matrix}\right.\) thì phương trình có 2 nghiệm phân biệt
c) Để phương trình có nghiệm kép \(\Leftrightarrow\Delta'=0\) \(\Leftrightarrow m=-9\)
\(\Rightarrow-9x^2+12x-4=0\) \(\Leftrightarrow x=\dfrac{2}{3}\)
Vậy \(m=-9\) thì phương trình có nghiệm kép \(x_1=x_2=\dfrac{2}{3}\)
d) Để phương trình vô nghiệm \(\Leftrightarrow\Delta'< 0\) \(\Leftrightarrow m< -9\)
Vậy \(m< -9\) thì phương trình vô nghiệm
a) 3x⁵ + 4x
Cho 3x⁵ + 4x = 0
x(3x⁴ + 4) = 0
x = 0 hoặc 3x⁴ + 4 = 0 (vô lý)
Vậy nghiệm của đa thức là x = 0
b) 9x¹⁰ - 7x⁹
Cho 9x¹⁰ - 7x⁹ = 0
x⁹(9x - 7) = 0
x⁹ = 0 hoặc 9x - 7 = 0
*) x⁹ = 0
x = 0
*) 9x - 7 = 0
9x = 7
x = 7/9
Vậy nghiệm của đa thức là x = 0; x = 7/9
c) x¹⁰⁰ - x⁹⁸
Cho x¹⁰⁰ - x⁹⁸ = 0
x⁹⁸(x² - 1) = 0
x⁹⁸ = 0 hoặc x² - 1 = 0
*) x⁹⁸ = 0
x = 0
*) x² - 1 = 0
x² = 1
x = 1 hoặc x = -1
Vậy nghiệm của đa thức là x = -1; x = 0; x = 1
e) Cho 2x²(3x - 2) + x(3x - 2) = 0
(3x - 2)(2x² + x) = 0
x(3x - 2)(2x + 1) = 0
x = 0 hoặc 3x - 2 = 0 hoặc 2x + 1 = 0
*) 3x - 2 = 0
3x = 2
x = 2/3
*) 2x + 1 = 0
2x = -1
x = -1/2
Vậy nghiệm của đa thức là x = -1/2; x = 0; x = 2/3
f) Cho (1 - x)(3 - x) - (1 - x)(3 + 2x) = 0
(1 - x)(3 - x - 3 - 2x) = 0
(1 - x)(-3x) = 0
-3x = 0 hoặc 1 - x = 0
*) -3x = 0
x = 0
*) 1 - x = 0
x = 1
Vậy nghiệm của đa thức là x = 0; x = 1
g) Cho 3(3 - x) + 1/3 (3 - x)² = 0
(3 - x)[3 + 1/3 (3 - x)] = 0
(3 - x)(3 + 1 - x/3) = 0
(3 - x)(4 - x/3) = 0
3 - x = 0 hoặc 4 - x/3 = 0
*) 3 - x = 0
x = 3
*) 4 - x/3 = 0
x/3 = 4
x = 12
Vậy nghiệm của đa thức là x = 3; x = 12
h) Cho x³ + x² + x + 1 = 0
(x³ + x²) + (x + 1) = 0
x²(x + 1) + (x + 1) = 0
(x + 1)(x² + 1) = 0
x + 1 = 0 hoặc x² + 1 = 0
*) x + 1 = 0
x = -1
*) x² + 1 = 0 (vô lý)
Vậy nghiệm của đa thức là x = -1