Cho tam giác ABC vuông tại B, đường cao BH = 12/5cm và 4AB=3BC. Tính AB,AC,BC,AH,CH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 10 2021
\(4AB=3BC\Leftrightarrow AB=\dfrac{3}{4}BC\)
Áp dụng HTL: \(AB^2=BH\cdot BC\Leftrightarrow\dfrac{9}{16}BC^2=\dfrac{12}{5}BC\Leftrightarrow BC\left(\dfrac{9}{16}BC-\dfrac{12}{5}\right)=0\\ \Leftrightarrow BC=\dfrac{12}{5}:\dfrac{9}{16}=\dfrac{64}{15}\left(cm\right)\\ \Leftrightarrow AB=\dfrac{16}{5}\left(cm\right)\)
Áp dụng HTL và PTG: \(\left\{{}\begin{matrix}AC=\sqrt{BC^2-AB^2}=\dfrac{16\sqrt{7}}{15}\left(cm\right)\\CH=\dfrac{AC^2}{BC}=\dfrac{28}{15}\left(cm\right)\end{matrix}\right.\)
19 tháng 9 2021
\(1,\)
\(a,\) Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AH^2=CH\cdot BH\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AH^2}{CH}=\dfrac{25}{6}\left(cm\right)\\AB=\sqrt{\dfrac{25}{6}\left(\dfrac{25}{6}+6\right)}=\dfrac{5\sqrt{61}}{6}\left(cm\right)\\AC=\sqrt{6\left(\dfrac{25}{6}+6\right)}=\sqrt{61}\left(cm\right)\end{matrix}\right.\\ BC=\dfrac{25}{6}+6=\dfrac{61}{6}\left(cm\right)\)
\(b,S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot5\cdot\dfrac{61}{6}=\dfrac{305}{12}\left(cm^2\right)\)
CM
30 tháng 9 2018
a, HB = 1,8cm; CH = 3,2cm; AH = 2,4cm; AC = 4cm
b, AB = 65cm; AC = 156cm; BC = 169cm; BH = 25cm
c, AB = 5cm; BC = 13cm; BH = 25/13cm; CH = 144/13cm
CM
10 tháng 1 2019
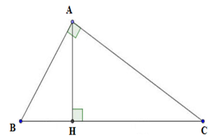
Xét tam giác ABC vuông tại A
+ Theo định lý Pytago ta có:
+ Theo hệ thức lượng trong tam giác vuông ta có:
A B 2 = BH. BC => BH = A B 2 B C = 3 2 5 = 9 5 = 1 , 8 c m
Mà BH + CH = BC => CH = BC – BH = 5 – 1,8 = 3,2 cm
Lại có AH. BC = AB.AC => AH = A B . A C B C = 3.4 5 = 2,4cm
Vậy BH = 1,8cm, CH = 3,2cm, AC = 4cm, AH = 2,4 cm
Đáp án cần chọn là: B
23 tháng 8 2021
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=16\)
hay AC=4cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=1.8cm\\CH=3.2cm\\AH=2.4cm\end{matrix}\right.\)
23 tháng 8 2021
Xét tam giác ABC vuông tại A
+ Theo định lý Pytago ta có:
+ Theo hệ thức lượng trong tam giác vuông ta có:
A B 2 = BH. BC => BH = A B 2 B C = 3 2 5 = 9 5 = 1 , 8 c m
Mà BH + CH = BC => CH = BC – BH = 5 – 1,8 = 3,2 cm
Lại có AH. BC = AB.AC => AH = A B . A C B C = 3.4 5 = 2,4cm
Vậy BH = 1,8cm, CH = 3,2cm, AC = 4cm, AH = 2,4 cm
7 tháng 1 2022
a.
Xét tam giác ABC vuông tại A, có:
AB^2 + AC^2 = BC^2 (Định Lý Pytago) => BC^2 = 25+144 = 169
=> BC = 13 (cm)
sinB = AC/BC = 12/13 => B = 67.4 (độ)
TA
1
12 tháng 9 2023
Xét ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC
=>HB*HC=4
BH+CH=5
=>BH=5-CH
HB*HC=4
=>HC(5-CH)=4
=>5HC-HC^2-4=0
=>HC^2-5HC+4=0
=>HC=1cm hoặc HC=4cm
TH1: HC=1cm
=>HB=4cm
\(AB=\sqrt{4\cdot5}=2\sqrt{5}\left(cm\right);AC=\sqrt{1\cdot5}=\sqrt{5}\left(cm\right)\)
TH2: HC=4cm
=>HB=1cm
\(AB=\sqrt{1\cdot5}=\sqrt{5}\left(cm\right);AC=\sqrt{4\cdot5}=2\sqrt{5}\left(cm\right)\)
26 tháng 7 2020
Mik gọi như này nhé, từ trung điểm M của BC, kẻ vuông góc với BC cắt AC tại N và AB tại K.
Bài làm
a) Xét tam giác ABC vuông tại A có:
\(BC=\sqrt{AB^2+AC^2}\)
hay \(BC=\sqrt{5^2+12^2}=\sqrt{25+144}\)
=> \(BC=\sqrt{169}=13\left(cm\right)\)
=> \(BM=MC=\frac{BC}{2}=\frac{13}{2}=6,5\left(cm\right)\)
Xét tam giác ABC và tam giác MNC có:
\(\widehat{BAC}=\widehat{NMC}=90^0\)
\(\widehat{C}\)chung
=> Tam giác ABC ~ tam giác MNC ( g-g )
=> \(\frac{AB}{MN}=\frac{AC}{MC}\)
hay \(\frac{5}{MN}=\frac{12}{6,5}\Rightarrow MN=\frac{65}{24}\left(cm\right)\)
b) Xét tam giác ABC vuông tại A
Đường cao AH
=> \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
hay \(\frac{1}{AH^2}=\frac{1}{5^2}+\frac{1}{12^2}\)
=> \(\frac{1}{AH^2}=\frac{1}{25}+\frac{1}{144}\)
=> \(\frac{1}{AH^2}=\frac{169}{3600}\)
=> \(AH^2=\frac{3600}{169}\)
=> \(AH=\sqrt{\frac{3600}{169}}=\frac{60}{13}\)( cm )
Xét tam giác AHB vuông tại H có:
Theo Pytago có:
\(BH^2=AB^2-AH^2\)
hay \(BH^2=5^2-\frac{3600}{169}\)
=> \(BH^2=25-\frac{3600}{169}\)
=>\(BH^2=\frac{625}{169}\)
=> \(BH=\frac{25}{13}\)( cm )
Ta có: BH + HC = BC
hay \(\frac{25}{13}+HC=13\)
=> \(HC=13-\frac{25}{13}\)
=> \(HC=\frac{144}{13}\)
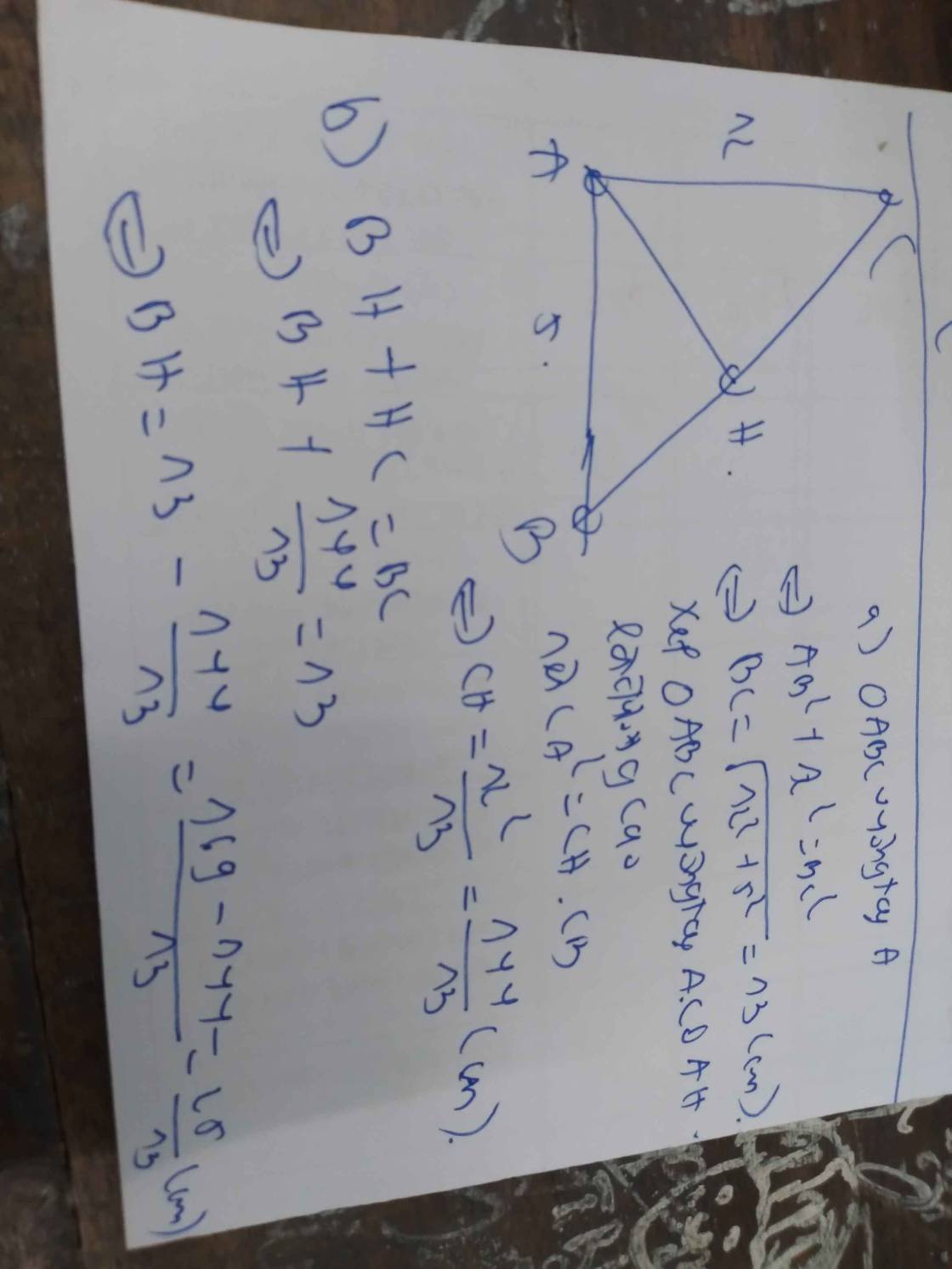
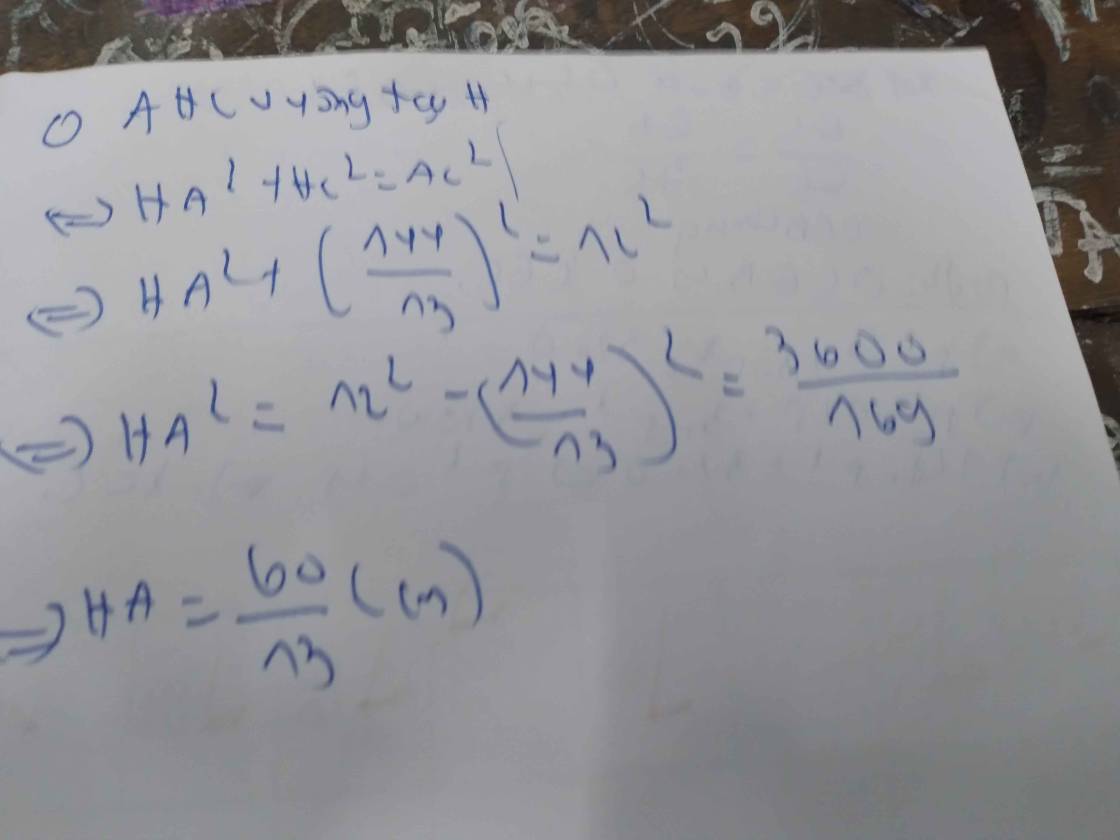
Có \(4AB=3BC\Rightarrow BC=\dfrac{4AB}{3}\)
+) Tam giác ABC vuông tại B có:
\(AC^2=AB^2+BC^2\left(pytago\right)\)
\(\Rightarrow AC=\sqrt{AB^2+BC^2}=\sqrt{AB^2+\left(\dfrac{4AB}{3}\right)^2}=\dfrac{5AB}{3}\)
+) Tam giác ABC vuông tại B, đường cao BH có:
\(AB.BC=BH.AC\\\Leftrightarrow AB.\dfrac{4AB}{3}=\dfrac{12}{5}.\dfrac{5AB}{3}\\ \Rightarrow AB=3\left(cm\right) \)
\(\Rightarrow BC=\dfrac{4AB}{3}=\dfrac{4.3}{3}=4\left(cm\right),AC=\dfrac{5AB}{3}=\dfrac{5.3}{3}=5\left(cm\right)\)
-) Có: \(AB^2=AH.AC\) (hệ thức lượng)
\(\Leftrightarrow3^2=AH.5\\ \Rightarrow AH=\dfrac{9}{5}\left(cm\right)\)
-) Có: \(BC^2=CH.AC\) (hệ thức lượng)
\(\Leftrightarrow4^2=CH.5\\ \Rightarrow CH=\dfrac{16}{5}\left(cm\right)\)
4AB=3BC
=>AB/3=BC/4=k
=>AB=3k; BC=4k
1/BA^2+1/BC^2=1/BH^2=1/2,4^2
=>k=1
=>AB=3cm; BC=4cm
AC=căn 3^2+4^2=5cm
AH=3^2/5=1,8cm
CH=5-1,8=3,2cm