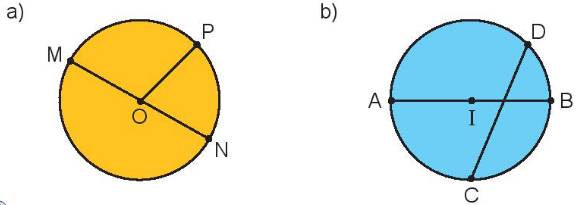
Tìm tâm, bán kính, đường kính của mỗi hình tròn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tâm, bán kính, đường kính của hình tròn bé lần lượt là:
B; BA; AC.
Tâm, bán kính, đường kính của hình tròn lớn lần lượt là:
C; CA; AD.

Sau khi vẽ ta được hình như sau:
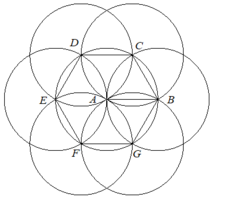
Khi đó, các đoạn thẳng A B = B C = C D = D E = E F = F G = G B (vì cùng bằng bán kính).

Gọi bán kính hình tròn tâm \(A\) và \(B\) lần lượt là \(x;y\left(m\right),\left(0< y< x< 3\right)\)
Vì 2 đường tròn tiếp xúc ngoài với nhau nên \(x+u=AB=3\left(m\right)\left(1\right)\)
Diện tích của hai vườn hoa hình tròn tâm \(A\) và \(B\) lần lượt là :,\(\text{π}x^2\left(m^2\right);\text{π}y^2\left(m^2\right)\)
Lại có diện tích bồn hoa bằng tổng diện tích của hai hình tròn bằng \(4,68\text{π}\left(m^2\right)\) nên :
\(\text{π}.x^2+\text{π}.y^2=4,68\text{π}\left(m^2\right)\Rightarrow x^2+y^2=4,68\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y=3\\x^2+y^2=4,68\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=3-y\\\left(3-y\right)^2+y^2=4,68\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=3-y\\2y^2+6y+4,32=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3-y\\\left(9y-5\right)\left(6y-5\right)=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=3-y\\\left[{}\begin{matrix}x=1,8\\y=1,2\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1,8\\y=1,2\end{matrix}\right.\\\left\{{}\begin{matrix}x=1,2\\y=1,8\end{matrix}\right.\end{matrix}\right.\)
Vậy bán kính của hai khu vường hình tròn tâm A và B lần lượt là 1,2 m và 1,8 m
a) Hình tròn tâm O; bán kính OM, ON, OP; đường kính MN.
b) Hình tròn tâm I; bán kính IA IB; đường kính AB.