Cho đường tròn tâm O, đường kính BC. Trên nửa đường tròn (O) lấy điểm A (A khác B và C), gọi H là hình chiếu của 4 trên BC. Trên cung AC của nửa đường tròn (O) lấy điểm D (D khác A và C), gọi E là hình chiếu của 4 trên BD, I là giao điểm của hai đường thẳng AH và BD.
a) Chứng minh tứ giác ABHE nội tiếp;
b) Chứng minh BI.BD = BH.BC;
c) Chứng minh hai tam giác AHE và ACD đồng dạng;
d) Hai đường thẳng AE và DH cắt nhau tại F. Chứng minh IF || AD.


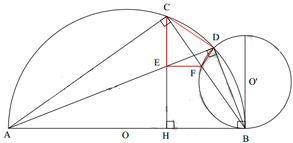


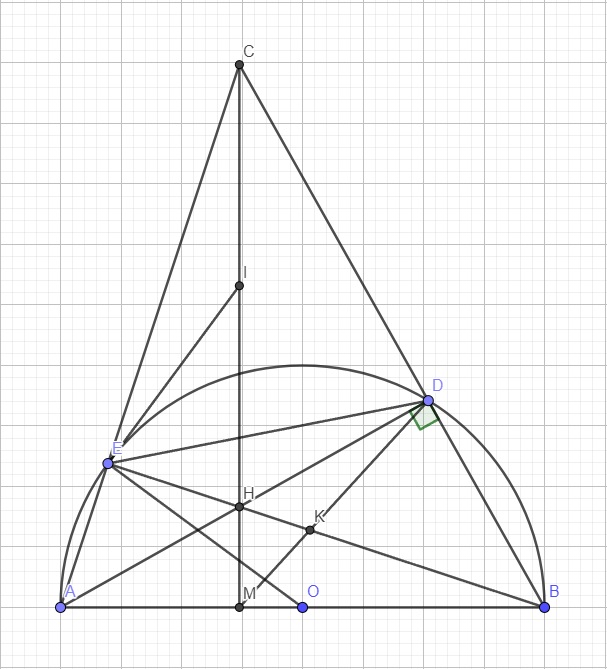
a/ H và E cùng nhìn AB dưới 1 góc vuông => ABHE là tứ giác nội tiếp
b/
\(\widehat{BDC}=90^o\) (góc nội tiếp chắn nửa đường tròn)
Xét tg vuông BHI và tg vuông BDC có
\(\widehat{DBC}\) chung => tg BHI đồng dạng với tg BDC
\(\Rightarrow\dfrac{BI}{BC}=\dfrac{BH}{BD}\Rightarrow BI.BD=BH.BC\)
c/
Xét tứ giác nội tiếp ABHE có
\(\widehat{HAE}=\widehat{CBD}\) (góc nt cùng chắn cung HE) (1)
\(\widehat{AHE}=\widehat{ABD}\) (góc nt cùng chắn cung AE) (2)
Xét (O) có
\(\widehat{CBD}=\widehat{CAD}\) (góc nt cùng chắn cung CD) (3)
\(\widehat{ABD}=\widehat{ACD}\) (góc nt cùng chắn cung AD) (4)
Từ (1) và (3) \(\Rightarrow\widehat{HAE}=\widehat{CAD}\) (5)
Từ (2) và (4) \(\Rightarrow\widehat{AHE}=\widehat{ACD}\) (6)
Từ (5) và (6) => tg AHE đồng dạng với tg ACD (g.g.g)
d/