Từ một điểm M nằm ngoài đường tròn (O;R). Vẽ hai tiếp tuyến MA,MB ( A,B là tiếp điểm) và một cát tuyến M cắt đường tròn tại C,D (C nằm giữa M và D). Gọi E là giao điểm của AB và OM.
1, Chứng minh MC.MD=ME.MO
2, giả sử OM=3R. Tìm diện tích lớn nhất của tứ giác MADB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Câu a),b) tự làm nhé , mình chỉ giúp câu c) thôi .
OI vuông góc NP ( Do I là trung điểm của MP ) , OF vuông góc NP ( Do OF là đường trung trực của NP )
=> O,I,F thẳng hàng
Tam giác ONF vuông tại N , đường cao NI
=> ON^2 = OI.OF
Mà ON=OA
OA^2 = OH.OM
=> OH.OM=OI.OF
=> OH/OI=OF/OM
Xét tam giác OIM và tam giác OHF có
góc MOF chung
OH/OI=OF/OM
=> Tam giác OIM đồng dạng tam giác OHF
=> góc OHF=góc OIM (=90 độ )
OH vuông HF
mà OH vuông AB
=> A,B,F thẳng hàng
=> F nằm trên đường thẳng cố định AB khi đường thẳng d quay quanh M mà vẫn thỏa mãn các yêu cầu đề bài
Điều phải chứng minh

a: Xét tứ giác MBOC có \(\widehat{MBO}+\widehat{MCO}=90^0+90^0=180^0\)
=>MBOC là tứ giác nội tiếp
=>M,B,O,C cùng thuộc một đường tròn
b: Sửa đề: \(CH\cdot HB=OH\cdot HM\)
Xét (O) có
MB,MC là các tiếp tuyến
Do đó: MB=MC
=>M nằm trên đường trung trực của BC(1)
ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra MO là đường trung trực của BC
=>MO\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOBM vuông tại B có BH là đường cao
nên \(OH\cdot HM=HB^2\)
=>\(OH\cdot HM=HB\cdot HC\)

Do \(OB=OE=R\Rightarrow\Delta OBE\) cân tại O
Mà \(OH\perp BE\) (giả thiết) \(\Rightarrow OH\) là đường cao đồng thời là trung trực của BE
Hay OA là trung trực của BE
\(\Rightarrow AB=AE\)
Xét hai tam giác OAB và OAE có: \(\left\{{}\begin{matrix}OB=OE=R\\AB=AE\left(cmt\right)\\OA\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OAB=\Delta OAE\left(c.c.c\right)\)
\(\Rightarrow\widehat{AEO}=\widehat{ABO}=90^0\Rightarrow AE\) là tiếp tuyến của (O)

a: Xét tứ giác OMAN có
\(\widehat{OMA}+\widehat{ONA}=180^0\)
Do đó: OMAN là tứ giác nội tiếp

a. Câu này đơn giản em tự giải.
b.
Ta có: \(\left\{{}\begin{matrix}OB=OC=R\\MB=MC\left(\text{t/c hai tiếp tuyến cắt nhau}\right)\end{matrix}\right.\)
\(\Rightarrow OM\) là trung trực của BC
\(\Rightarrow OM\perp BC\) tại H đồng thời H là trung điểm BC hay \(HB=HC\)
\(OC\perp MC\) (MC là tiếp tuyến tại C) \(\Rightarrow\Delta OMC\) vuông tại C
Áp dụng hệ thức lượng trong tam giác vuông OMC với đường cao CH:
\(CH^2=OH.MH\)
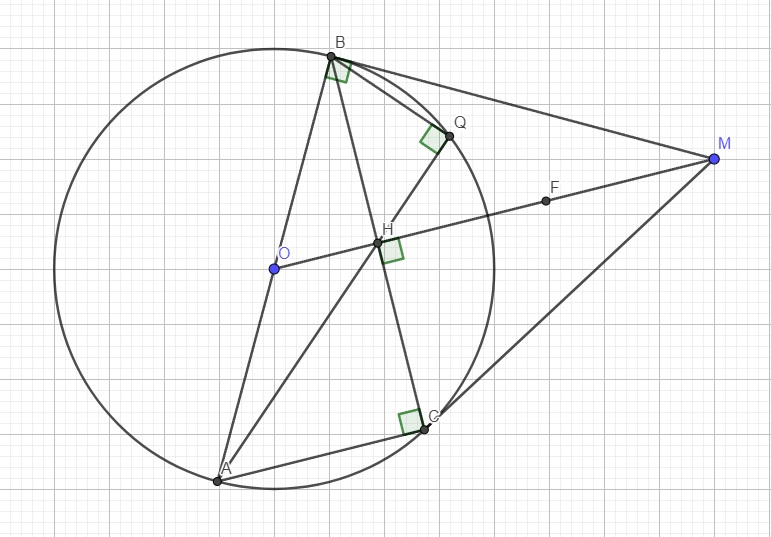
c.
C nằm trên đường tròn và AB là đường kính \(\Rightarrow\widehat{ACB}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{ACB}=90^0\)
Xét hai tam giác MBH và BAC có:
\(\left\{{}\begin{matrix}\widehat{MHB}=\widehat{ACB}=90^0\\\widehat{MBH}=\widehat{BAC}\left(\text{cùng chắn BC}\right)\end{matrix}\right.\) \(\Rightarrow\Delta MBH\sim\Delta BAC\left(g.g\right)\)
\(\Rightarrow\dfrac{BH}{AC}=\dfrac{MH}{BC}\Rightarrow\dfrac{BH}{AC}=\dfrac{2HF}{2CH}\) (do F là trung điểm MH và H là trung điểm BC)
\(\Rightarrow\dfrac{BH}{AC}=\dfrac{HF}{CH}\)
Xét hai tam giác BHF và ACH có:
\(\left\{{}\begin{matrix}\dfrac{BH}{AC}=\dfrac{HF}{CH}\left(cmt\right)\\\widehat{BHF}=\widehat{ACH}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta BHF\sim\Delta ACH\left(c.g.c\right)\)
\(\Rightarrow\widehat{HBF}=\widehat{CAH}\)
Mà \(\widehat{CAH}=\widehat{CBQ}\) (cùng chắn CQ)
\(\Rightarrow\widehat{HBF}=\widehat{CBQ}\) hay \(\widehat{HBF}=\widehat{HBQ}\)
\(\Rightarrow B,Q,F\) thẳng hàng