Cho M = (2sqrt(a) + 2)/(sqrt(a) + 5) tìm số hữu tỉa để M nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: \(A=\dfrac{x\sqrt{x}+1}{x+2\sqrt{x}+1}\)
ĐKXĐ: x>=0
\(A=\dfrac{x\sqrt{x}+1}{x+2\sqrt{x}+1}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2}\)
\(=\dfrac{x-\sqrt{x}+1}{\sqrt{x}+1}\)
Thay x=4 vào A, ta được:
\(A=\dfrac{4-2+1}{2+1}=\dfrac{5-2}{3}=1\)
b: M=A*B
\(=\dfrac{x-\sqrt{x}+1}{\sqrt{x}+1}\cdot\left(\dfrac{2x+6\sqrt{x}+7}{x\sqrt{x}+1}-\dfrac{1}{\sqrt{x}+1}\right)\)
\(=\dfrac{x-\sqrt{x}+1}{\sqrt{x}+1}\cdot\left(\dfrac{2x+6\sqrt{x}+7}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}+1}\right)\)
\(=\dfrac{x-\sqrt{x}+1}{\sqrt{x}+1}\cdot\dfrac{2x+6\sqrt{x}+7-x+\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{x-\sqrt{x}+1}{\sqrt{x}+1}\cdot\dfrac{x+7\sqrt{x}+6}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+6\right)}{\left(\sqrt{x}+1\right)^2}=\dfrac{\sqrt{x}+6}{\sqrt{x}+1}\)
Để M>2 thì M-2>0
=>\(\dfrac{\sqrt{x}+6-2\sqrt{x}-2}{\sqrt{x}+1}>0\)
=>\(-\sqrt{x}+4>0\)
=>\(-\sqrt{x}>-4\)
=>\(\sqrt{x}< 4\)
=>0<=x<16
c: Để M là số nguyên thì \(\sqrt{x}+6⋮\sqrt{x}+1\)
=>\(\sqrt{x}+1+5⋮\sqrt{x}+1\)
=>\(5⋮\sqrt{x}+1\)
=>\(\sqrt{x}+1\in\left\{1;-1;5;-5\right\}\)
=>\(\sqrt{x}\in\left\{0;-2;4;-6\right\}\)
=>\(\sqrt{x}\in\left\{0;4\right\}\)
=>\(x\in\left\{0;16\right\}\)

1: \(A=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right)\cdot\left(\dfrac{x-\sqrt{x}}{2\sqrt{x}+1}\right)\)
\(=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{2\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}+1+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{2\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
2: Thay x=9 vào A, ta được:
\(A=\dfrac{3}{3+1}=\dfrac{3}{4}\)

Ta có \(M=\frac{\sqrt{a}+2}{\sqrt{a}-2}=\frac{\sqrt{a}-2}{\sqrt{a}-2}+\frac{4}{\sqrt{a}-2}=1+\frac{4}{\sqrt{a}-2}\)
Để M nguyên thì \(\frac{4}{\sqrt{a}-2}\)nguyên
Ta có bảng sau:
| \(\sqrt{a}\)-2 | 1 | -1 | 2 | -2 | 4 | -4 |
| a | Loại | 1 | 16 | 0 | Loại | Loại |
Vậy tại a là 0;16;2 thì M nguyên

Ta có : \(M=\frac{\sqrt{x}+6}{\sqrt{x}+1}=\frac{\sqrt{x}+1+5}{\sqrt{x}+1}=\frac{\sqrt{x}+1}{\sqrt{x}+1}+\frac{5}{\sqrt{x}+1}=1+\frac{5}{\sqrt{x}+1}\)
Để M nguyên thì 5 chia hết cho \(\sqrt{x}+1\)
Nên : \(\sqrt{x}+1\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\)
Ta có bảng :
| \(\sqrt{x}+1\) | -5 | -1 | 1 | 5 |
| \(\sqrt{x}\) | -6 (loại) | -2(loại | 0 | 4 |
| x | 0 | 2 |
bài có nhầm đề không bạn? vì tử = mẫu thì M=1 rồi kìa

\(M=\dfrac{\sqrt{a}+2}{\sqrt{a}-2}=\dfrac{\sqrt{a}-2}{\sqrt{a}-2}+\dfrac{4}{\sqrt{a}-2}=1+\dfrac{4}{\sqrt{a}-2}\in Z\)
\(\Rightarrow\sqrt{a}-2\inƯ\left(4\right)=\left\{1;-1;2;-2;4;-4\right\}\)
Do \(\sqrt{a}\ge0\)
\(\Leftrightarrow\sqrt{a}\in\left\{3;1;4;0;6\right\}\)
\(\Rightarrow a\in\left\{9;1;16;0;36\right\}\)
Đề yêu cầu tìm a nguyên thì đúng hơn.
Vì yêu cầu tìm a hữu tỉ bài này sẽ có vô số số hữu tỉ thỏa mãn

a: Để M là số nguyên thì 5 chia hết cho căn a+1
=>căn a+1 thuộc {1;5}
=>a thuộc {0;4}
b: Khi a=4/9 thì \(M=1+\dfrac{5}{\dfrac{2}{3}+1}=1+5:\dfrac{5}{3}=1+3=4\)
=>M là số nguyên
c: \(\sqrt{a}+1>=1\)
=>\(\dfrac{5}{\sqrt{a}+1}< =5\)
=>M<=6
\(1< =\dfrac{5}{\sqrt{a}+1}< =5\)
=>2<=M<=6
M=2 khi \(\dfrac{5}{\sqrt{a}+1}+1=2\)
=>\(\dfrac{5}{\sqrt{a}+1}=1\)
=>căn a+1=5
=>căn a=4
=>a=16
M=3 khi \(\dfrac{5}{\sqrt{a}+1}=2\)
=>căn a+1=5/2
=>căn a=3/2
=>a=9/4
M=4 thì \(\dfrac{5}{\sqrt{a}+1}=3\)
=>căn a+1=5/3
=>căn a=2/3
=>a=4/9
\(M=5\Leftrightarrow\dfrac{5}{\sqrt{a}+1}=4\)
=>căn a+1=5/4
=>căn a=1/4
=>a=1/16
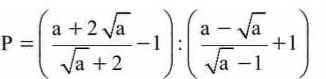 Bài 4. Cho biểu thức: P = ((a + 2sqrt(a))/(sqrt(a) + 2) - 1) / ((a - sqrt(a))/(sqrt(a) - 1) + 1)
Bài 4. Cho biểu thức: P = ((a + 2sqrt(a))/(sqrt(a) + 2) - 1) / ((a - sqrt(a))/(sqrt(a) - 1) + 1)