Cho CSC có: u1 + 2u5 = 0 và S4 = 14. Tính u10
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 5 2023
=>u1+3q-u1=6 và u1+10q=23
=>q=2 và u1=3
u12=u1+11*q=3+11*2=25
CM
9 tháng 1 2019
Chọn C.
Ta có: u23 + u57 = 29 ⇔ u1 + 22d + u1 + 56d = 29 ⇔ 2u1 + 78d = 29
Ta có: 3u1 + u10 + u70 + u157 = 3u1 + u1 +9d + u1 + 69d + u1 + 156d
= 6u1 + 234d = 3(2u1 + 78d) = 3.29 = 87
CM
13 tháng 9 2017
Đáp án B.
Đặt t = 2 + log u 1 - 2 log u 10 ≥ 0
⇔ 2 log u 1 - 2 log u 10 = t 2 - 2 ,
khi đó giả thiết trở thành:
log u 1 - 2 log u 10 + 2 + log u 1 - 2 log u 10 = 0
⇔ t 2 + t - 2 = 0
<=> t = 1 hoặc t = -2
⇒ log u 1 - 2 log u 10 = - 1
⇔ log u 1 + 1 = 2 log u 10
⇔ log 10 u 1 = log u 10 2 ⇔ 10 u 1 = u 10 2 ( 1 )
Mà un+1 = 2un => un là cấp số nhân với công bội q = 2
=> u10 = 29 u1 (2)
Từ (1), (2) suy ra
10 u 1 = 9 9 u 1 2 ⇔ 2 18 u 1 2 = 10 u 1 ⇔ u 1 = 10 2 18
⇒ u n = 2 n - 1 . 10 2 18 = 2 n . 10 2 19 .
Do đó u n > 5 100 ⇔ 2 n . 10 2 19 > 5 100
⇔ n > log 2 5 100 . 2 19 10 = - log 2 10 + 100 log 2 5 + 19 ≈ 247 , 87
Vậy giá trị n nhỏ nhất thỏa mãn là n = 248.
C
0
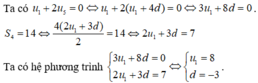
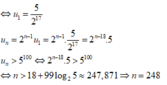
=>u1+2(u1+4d)=0 và 4*(2u1+3d)/2=14
=>3u1+8d=0 và 2u1+3d=7
=>u1=8; d=-3
u10=u1+9d=8-27=-19