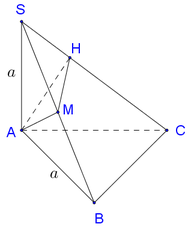
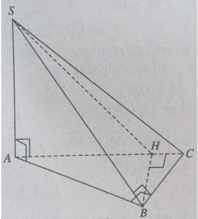
1/ Cho hình chóp S.ABC: SA vuông góc với (ABC), ΔABC vuông tại B, AB=4a, BC=3a, SA=\(a\sqrt{2}\). H là chân d cao kẻ từ A xuống SA.
a. CMR: BC vuông góc với (SAB)
b. Tính d(B;(SAC))
c. Tính d(AH;SC)
2/ Cho hình chóp S.ABCD: ABCD là hình vuông tâm O. SO vuông góc với (ABCD), AB=2a, SO=4a
a. CMR: BD vuông góc với (SAC)
b. Tính d(O;(SCD))
c. Tính d(AB;SD)
CỨU E VS M.N ƠI, mai kt 15' nx mà thật sự ko bt lm, giúp e vs, cảm ơn ạ



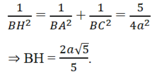
1:
a: BC vuông góc BA
BC vuông góc SA
=>BC vuông góc (SAB)
b: Kẻ BK vuông góc AC, BH vuông góc SK
=>BH=d(B;(SAC))
\(AC=\sqrt{BA^2+BC^2}=5a\)
AK=(4a)^2/5a=3,2a
BK=4a*3a/5a=2,4a
\(SB=\sqrt{2a^2+16a^2}=3a\sqrt{2}\)
SK=căn 2a^2+10,24a^2=a*3căn 34/5
BK=2,4a
SK^2+BK^2=SB^2
nên ΔSKB vuông tại K
=>K trùng với H
=>d(B;(SAC))=BK=2,4a