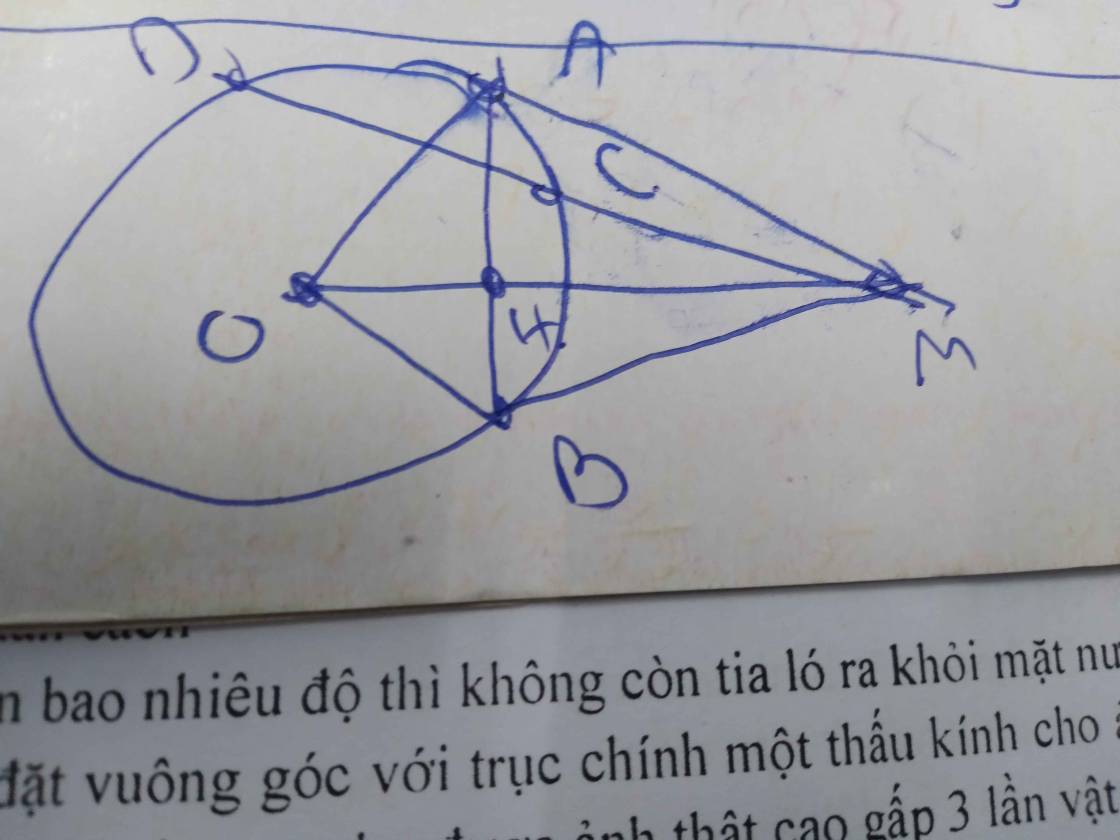
Từ điểm M nằm ngoài đường tròn (O), kẻ 2 tiếp tuyến MA; MB. Tia Mx, nằm giữa hai tia MA và MO cắt (0) tại C và D và cắt AB tại N. Gọi K là trung điểm CD; H là giao điểm AB và OM.
a) Chứng minh OKNH nội tiếp b) Chứng minh MC.MD= MN.MK
c) Chứng minh BCK và BAD đồng dạng
d) Đường thắng qua H vuông góc OA cắt AC và AD tại E và F. Chứng minh HE = HF
giup minh cau d nha



d: CK/AD=CB/AB
=>AD*CB=CK*AB=AB*DK
=>DK/CB=AD/AB
=>ΔBCA đồng dạng với ΔDKA
=>góc BAC=góc DAK
AM vuông góc OA
EF vuông góc OA
=>AM//EF
=>góc AEF=góc MAC=góc ADC
=>ΔADC đồng dạng với ΔAEF
=>CD/EF=AD/AE
góc EAH=góc KAD; góc AEH=góc ADK
=>ΔAEH đồng dạng với ΔADK
=>DK/EH=AD/AE
=>CD/EF=DK/EH
=>EH=FH