a= (-7x). (-1/7x^5)( -x^2) thu gọn đơn thức
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ON
4 tháng 7 2018
a)A=\(x^5-\dfrac{1}{2}x+7x^3-2x+\dfrac{1}{5}x^3+3x^4-x^5+\dfrac{2}{5}x^4+15\)
=\(=\dfrac{-5}{2}x+\dfrac{36}{5}x^3+\dfrac{17}{5}x^4+15\)
b)B=\(3x^2-10+\dfrac{2}{5}x^3+7x-x^2+8+7x^2\)
\(=9x^2+\dfrac{2}{5}x^3+7x+2\)
c)C=\(\dfrac{1}{7}x-2x^4+5x+6\)
B
1
17 tháng 7 2023
\(\dfrac{5}{7}x^3.\dfrac{2}{3}x^4.\left(-\dfrac{7}{10}x\right)\)
\(=\dfrac{5}{7}.\dfrac{2}{3}.\left(-\dfrac{7}{10}\right).\left(x^3.x^4.x\right)\)
\(=-\dfrac{1}{3}x^8\)
+ Phần hệ số: \(-\dfrac{1}{3}\)
+ Phần biến: \(x^8\)
9 tháng 4 2021
Bài 1:
a) Ta có: \(-ax\left(xy^3\right)^2\cdot\left(-by\right)^3\)
\(=-a\cdot x\cdot x^2\cdot y^6\cdot\left(-b\right)^3\cdot y^3\)
\(=abx^3y^9\)
b) Ta có: \(xy\cdot\left(-ax\right)^2\cdot\left(-by\right)^3\)
\(=xy\cdot a^2\cdot x^2\cdot b^3\cdot y^3\)
\(=a^2b^3x^3y^4\)
9 tháng 4 2021
Bài 2:
Ta có: \(P\left(x\right)=5x-4x^4+x^6+3-2x^3-7x-x^7+1-2x^6+3x^3+x^7\)
\(=\left(-x^7+x^7\right)+\left(x^6-2x^6\right)-4x^4+\left(-2x^3+3x^3\right)+\left(5x-7x\right)+\left(3+1\right)\)
\(=-x^6-4x^4+x^3-2x+4\)
25 tháng 8 2021
a: Ta có: \(x^2-4x\left(3x-4\right)+7x-5\)
\(=x^2-12x^2+16x+7x-5\)
\(=-11x^2+23x-5\)
b: Ta có: \(7x\left(x^2-5\right)-3x^2y\left(xy-6y^2\right)\)
\(=7x^3-35x-3x^3y^2+18x^2y^3\)
c: Ta có: \(\left(5x+4\right)\left(2x-7\right)\)
\(=10x^2-35x+8x-28\)
\(=10x^2-27x-28\)
28 tháng 4 2017
a)A(x)=-(2x4+7x5-3x2)+2x4+7x5-2x2+1
=[-(2x4+7x5-3x2)+(2x4+7x5-3x2)]+x2+1
=x2+1
Vậy A(x)=x2+1
b)Để A(x)=G(x) thì x2+1=x2+x+2
<=>x=x2+1-x2-2
<=>x=-1
Vậy x=-1
c)A(x)=x2+1
Do x2\(\ge0\forall x\in R\)
=>x2+1>0\(\forall x\in R\)
=>A(x)>0\(\forall x\in R\)
=>A(x) vô nghiệm (đpcm)
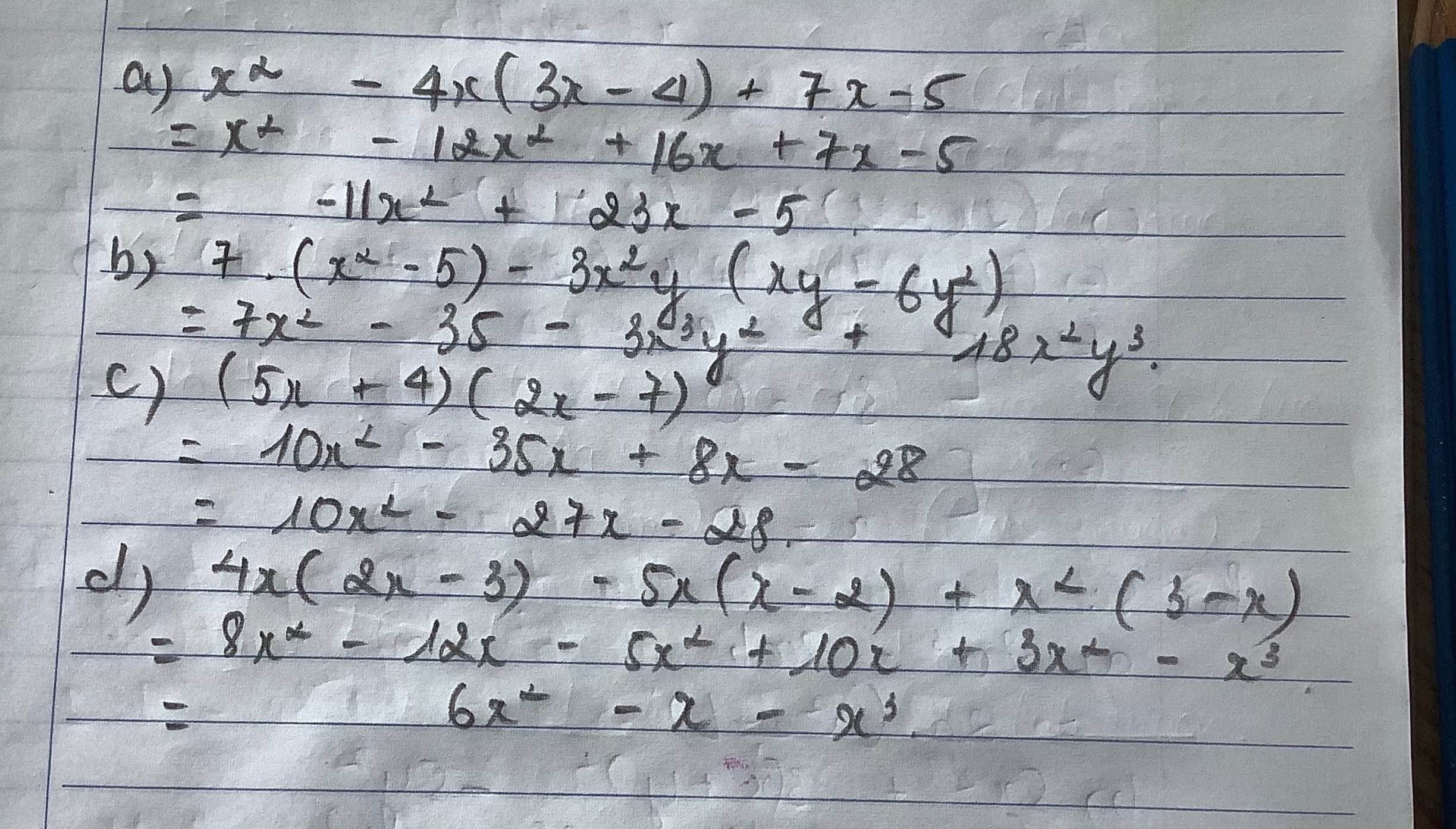
Ta có:
\(A\left(x\right)=\left(-7x\right).\left(-\dfrac{1}{7}x^5\right).\left(-x^2\right)\)
\(=-7x.\left(-\dfrac{1}{7}\right)x^5.\left(-1\right)x^2\)
\(=\left[-7.\left(-\dfrac{1}{7}\right).\left(-1\right)\right].\left(x.x^5.x^2\right)\)
\(=-1.x^8\)
\(=-x^8\)