Cho tam giác DEF cân tại D.Trên cạnh DE và DF lần lượt lấy 2 điểm H và K sao cho DH=ĐK.Gọi giáo điểm của EK và FH là O. Chứng minh rằng a EK=FH b tam giác HOE=tam giác KOF c DO vuông góc với EF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 4 2023
a) Ta có HE = DE - DH
KF = DF - DK
Mà DH = DK (gt)
và DE = DF ( △DEF cân tại D )
⇒ HE = KF
Xét △HEF và △KFE có:
HE = KF (cmt)
\(\widehat{HEF}\) = \(\widehat{KFE}\) ( △DEF cân tại D )
EF là cạnh chung
⇒ △HEF = △KFE ( c-g-c )
⇒ FH = EK ( 2 cạnh tương ứng )
b) Theo câu a có △HEF = △KFE
⇒ \(\widehat{OEF}\) = \(\widehat{OFE}\) ( 2 góc tương ứng )
Xét △OEF có:
\(\widehat{OEF}\) = \(\widehat{OFE}\) (cmt)
⇒ △OEF cân tại O
⇒ OE = OF
Ta có: \(\widehat{HEF}\) - \(\widehat{OEF}\) = \(\widehat{HEO}\)
và \(\widehat{KFE}\) - \(\widehat{OFE}\) = \(\widehat{KFO}\)
Lại có: \(\widehat{HEF}\) = \(\widehat{KFE}\) ; \(\widehat{OEF}\) = \(\widehat{OFE}\) (cmt)
⇒ \(\widehat{HEO}\) = \(\widehat{KFO}\)
Xét △HEO và △KFO có:
OE = OF (cmt)
\(\widehat{HEO}\) = \(\widehat{KFO}\) (cmt)
HE = KF ( theo a)
⇒ △HEO = △KFO (c-g-c)
c) Gọi A là giao điểm của DO và EF
Theo câu b có △HEO = △KFO
⇒ HO = OK ( 2 cạnh tương ứng )
Xét △HDO và △KDO có:
DH = DK (gt)
HO = OK (cmt)
DO là cạnh chung
⇒ △HDO = △KDO (c-c-c)
Xét △DCE và △DCF có:
DE = DF (△DEF cân tại D )
\(\widehat{EDC}\) = \(\widehat{FDC}\) (cmt)
DC là cạnh chung
⇒ △DCE = △DEF (c-g-c)
⇒ \(\widehat{DCE}\) = \(\widehat{DEF}\) ( 2 góc tương ứng )
Mà \(\widehat{DCE}\) = \(\widehat{DCF}\) = \(\dfrac{180^0}{2}\) = 900 hay DO \(\perp\) EF
.
30 tháng 4 2019
a)Xét\(\Delta DEF\)có:\(EF^2=DE^2+DF^2\)(Định lý Py-ta-go)
hay\(5^2=3^2+DF^2\)
\(\Rightarrow DF^2=5^2-3^2=25-9=16\)
\(\Rightarrow DF=\sqrt{16}=4\left(cm\right)\)
Ta có:\(DE=3cm\)
\(DF=4cm\)
\(EF=5cm\)
\(\Rightarrow DE< DF< EF\)hay\(3< 4< 5\)
b)Xét\(\Delta DEF\)và\(\Delta DKF\)có:
\(DE=DK\)(\(D\)là trung điểm của\(EK\))
\(\widehat{EDF}=\widehat{KDF}\left(=90^o\right)\)
\(DF\)là cạnh chung
Do đó:\(\Delta DEF=\Delta DKF\)(c-g-c)
\(\Rightarrow EF=KF\)(2 cạnh t/ứ)
Xét\(\Delta KEF\)có:\(EF=KF\left(cmt\right)\)
Do đó:\(\Delta KEF\)cân tại\(F\)(Định nghĩa\(\Delta\)cân)
c)Ta có:\(DF\)cắt\(EK\)tại\(D\)là trung điểm của\(EK\Rightarrow DF\)là đg trung tuyến xuất phát từ đỉnh\(F\)của\(\Delta KEF\)
\(KI\)cắt\(EF\)tại\(I\)là trung điểm của\(EF\Rightarrow KI\)là đg trung tuyến xuất phát từ đỉnh\(K\)của\(\Delta KEF\)
Ta lại có:\(DF\)cắt\(KI\)tại\(G\)
mà\(DF\)là đg trung tuyến xuất phát từ đỉnh\(F\)của\(\Delta KEF\)
\(KI\)là đg trung tuyến xuất phát từ đỉnh\(K\)của\(\Delta KEF\)
\(\Rightarrow G\)là trọng tâm của\(\Delta KEF\)
\(\Rightarrow GF=\frac{2}{3}DF\)(Định lí về TC của 3 đg trung tuyến của 1\(\Delta\))
\(=\frac{2}{3}.4=\frac{8}{3}\approx2,7\left(cm\right)\)
Vậy\(GF\approx2,7cm\)
NT
5 tháng 4 2021
a) Xét ∆ADB và ∆AEC có:
AB=AC (gt)
góc ABD= góc ACE (gt)
BD=CE(gt)
=>∆ADB=∆AEC(c.g.c0
=>AD=AC (2 cạnh tương ứng)
=>∆ADE là ∆cân tại A
b)Xét ∆BHD và ∆CKE có:
góc BHD=góc EHC=90
BD=CE(gt)
góc B=góc C(gt)
=>∆BHD=∆CKE(cạnh huyền góc nhọn)
=>DH=EK(2 cạnh tương ứng)(đpcm)
c)∆BHD=∆CKE(cmt) =>góc HDB =góc KEC (2cạnh tương ứng)
mà ∠HDB=∠EDO( đối đỉnh), ∠KEC=∠DEO(đối đỉnh)
=>∠EDO=∠DEO =>∆ODE cân tại O (đpcm)
14 tháng 2 2022
a: Ta có: ΔDEF cân tại D
mà DH là đường cao
nên H là trung điểm của EF
hay EH=FH
b: EH=FH=EF/2=3(cm)
Xét ΔDHE vuông tại H có \(DE^2=DH^2+HE^2\)
nên DH=4(cm)
c: Xét ΔDEM và ΔDFN có
DE=DF
\(\widehat{EDM}\) chung
DM=DN
Do đó: ΔDEM=ΔDFN
Suy ra: \(\widehat{DEM}=\widehat{DFN}\)
d: Xét ΔNEH và ΔMFH có
NE=MF
\(\widehat{E}=\widehat{F}\)
EH=FH
Do đó: ΔNEH=ΔMFH
Suy ra: HN=HM
hay H nằm trên đường trung trực của MN(1)
Ta có: KM=KN
nên K nằm trên đường trung trực của MN(2)
Ta có: DN=DM
nên D nằm trên đường trung trực của MN(3)
Từ (1), (2) và (3) suy ra D,H,K thẳng hàng
14 tháng 2 2022
a. xét tam giác DHE và tam giác DHF, có:
D: góc chung
DE = DF ( DEF cân )
DH: cạnh chung
Vậy tam giác DHE = tam giác DHF ( c.g.c )
=> HE = HF ( 2 cạnh tương ứng )
b.ta có: EH = EF :2 ( EF là đường cao cũng là trung tuyến ) = 6 : 2 =3 cm
áp dụng định lý pitago vào tam giác vuông DHE, có:
\(DE^2=DH^2+EH^2\)
\(\Rightarrow DH=\sqrt{DE^2-EH^2}=\sqrt{5^2-3^2}=\sqrt{16}=4cm\)
c.xét tam giác DEM và tam giác DFN có:
DE = DF ( DEF cân )
DM = DN ( gt )
D: góc chung
Vậy tam giác DEM = tam giác DFN ( c.g.c )
=> góc DEM = góc DFN ( 2 góc tương ứng )
d.xét tam giác DKM và tam giác DKN, có:
DM = DN ( gt )
D: góc chung
DK: cạnh chung
Vậy tam giác DKM = tam giác DKN ( c.g.c )
=> góc DKM = góc DKN = 90 độ ( tam giác BNM cân, K là trung điểm cũng là đường cao )
=> DK vuông BC
Mà DH cũng vuông BC
=> D,H,K thẳng hàng
Chúc bạn học tốt!!!
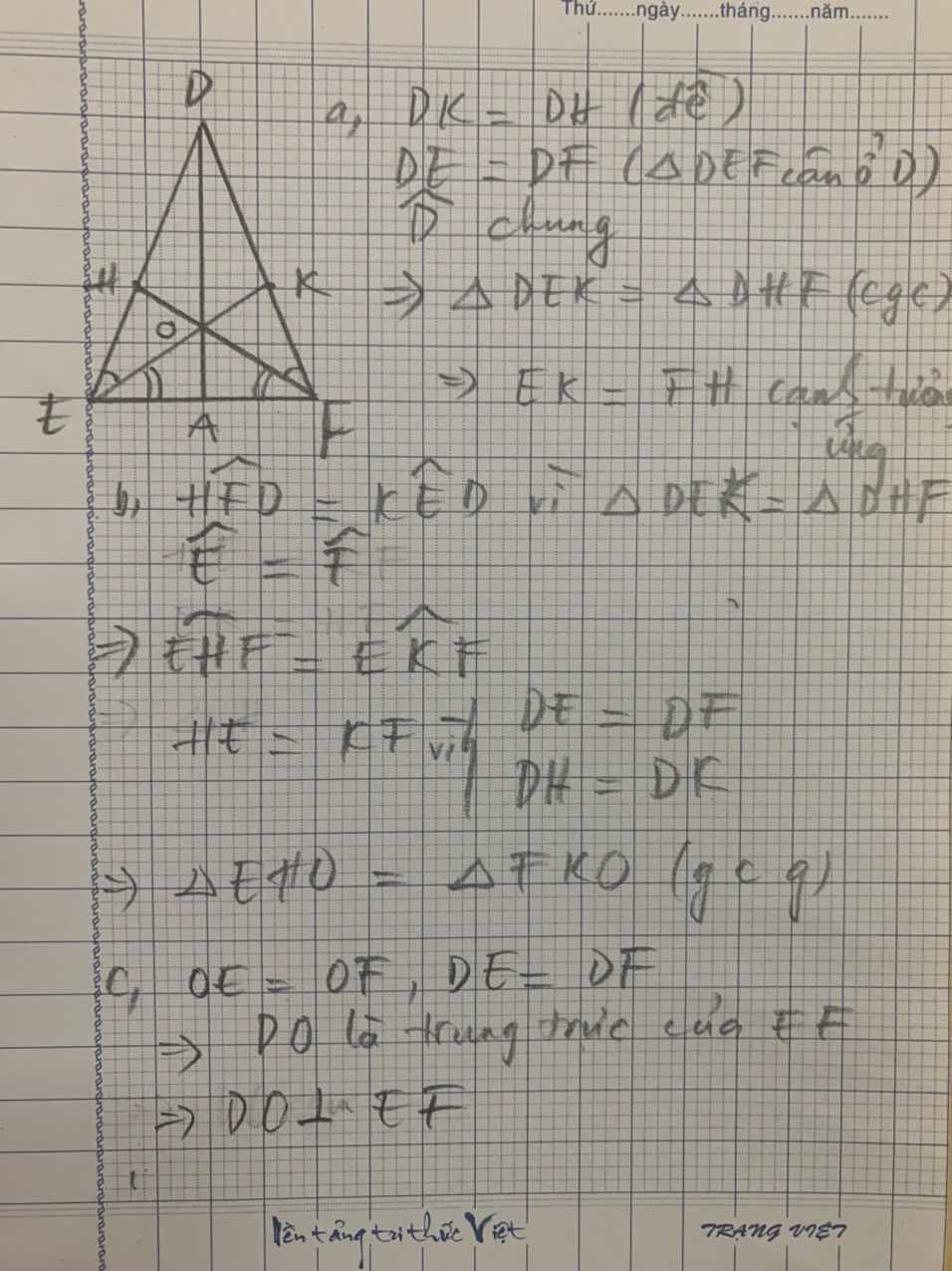
a: Xét ΔDKE và ΔDHF có
DK=DH
góc D chung
DE=DF
=>ΔDKE=ΔDHF
=>KE=HF
b: Xét ΔOHE và ΔOKF có
góc OHE=góc OKF
HE=KF
góc OEH=góc OFK
=>ΔOHE=ΔOKF
c: DE=DF
OE=OF
=>DO là trung trực của EF
=>DO vuông góc EF