một tkpk có tiêu cự 15 cm ,đặt vặt ab cao 5 cm vuông gốc với trục chính
a.vẽ a'b' và nêu tính chất của ảnh
b.tính chiều cao của ảnh và khoảng cách từ ảnh tới thấu kính
giúp mình với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
23 tháng 5 2022
câu a bạn tự vẽ nha mình biếng á
b) Ảnh thật vì là thấu kính hội tụ
c)
áp dụng công thức:
\(\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{f}\) <=> \(\dfrac{1}{20}+\dfrac{1}{d'}=\dfrac{1}{10}\)
=> \(d'=1:\left(\dfrac{1}{10}-\dfrac{1}{20}\right)=20cm\)
\(\dfrac{AB}{A'B'}=\dfrac{d}{d'}\Rightarrow A'B'=\dfrac{5.20}{20}=5cm\)
TM
18 tháng 4 2023
a) Bạn tự vẽ hình.
b) Hình minh họa :
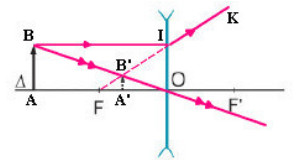
Xét \(\Delta FA'B'\sim\Delta FOI\) có : \(\dfrac{A'B'}{OI}=\dfrac{A'F}{OF}\Leftrightarrow\dfrac{A'B'}{AB}=\dfrac{OF-OA'}{OF}\)
\(\Rightarrow\dfrac{h'}{3}=\dfrac{15-d'}{15}\left(1\right)\)
Xét \(\Delta OA'B'\sim\Delta OAB\) có : \(\dfrac{A'B'}{AB}=\dfrac{OB'}{OB}\Leftrightarrow\dfrac{h'}{3}=\dfrac{d'}{30}\left(2\right)\).
Từ (1) và (2), ta có hệ phương trình : \(\left\{{}\begin{matrix}\dfrac{h'}{3}=\dfrac{15-d'}{15}\\\dfrac{h'}{3}=\dfrac{d'}{30}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d'=10\left(cm\right)\\h'=1\left(cm\right)\end{matrix}\right.\).
Vậy : Ảnh A'B' cách thấu kính \(d'=10\left(cm\right)\) và cao \(h'=1\left(cm\right)\).
19 tháng 3 2022
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{10}=\dfrac{1}{15}+\dfrac{1}{d'}\Rightarrow d'=30cm\)
H9
HT.Phong (9A5)
CTVHS
27 tháng 4 2023
a)
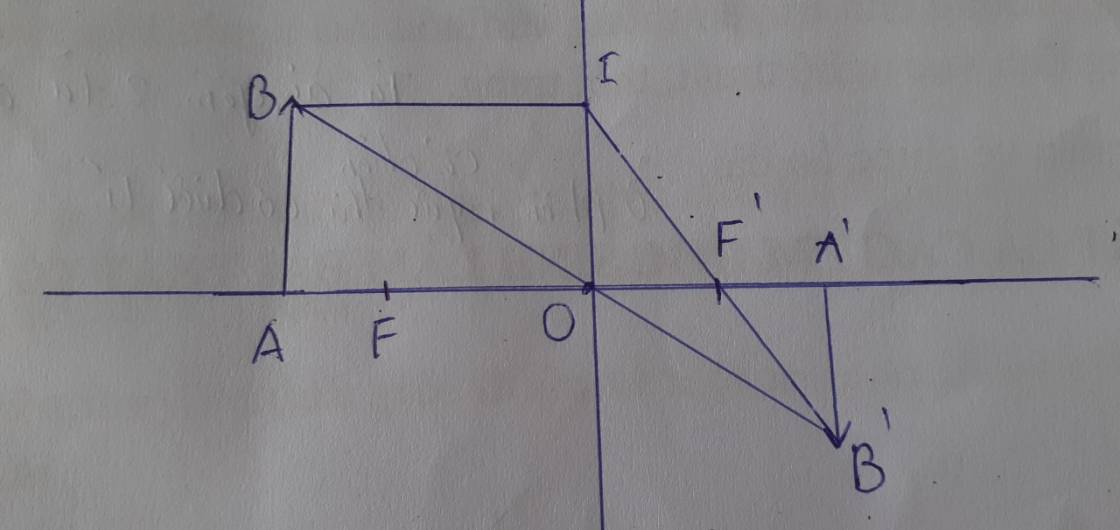
+ Vật AB cách thấu kính một khoảng d = 30 cm
Vì d > f = 10cm, nên ảnh A'B' là ảnh thật, ngược chiều và nhỏ hơn vật
b) Ta có: \(\dfrac{d}{d'}=\dfrac{h}{h'}\Leftrightarrow\dfrac{d}{h}=\dfrac{d'}{h'}\Rightarrow\dfrac{d'}{h'}=\dfrac{30}{2}\Leftrightarrow d'=15h'\)
Áp dụng công thức tính thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Leftrightarrow\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{15h'}\Rightarrow\dfrac{1}{10}=\dfrac{1}{30}+\dfrac{1}{15h'}\)
\(\Rightarrow h'=1\left(cm\right)\)
Vậy ảnh cao 1(cm)
Khoảng cách từ ảnh đến thấu kính:
\(d'=15h'=15.1=15\left(cm\right)\)