cho tam giác abc vuông tại a có ah là đường cao (h thuộc bc) .gọi d và e lần lượt là hình chiếu của h trên ab và ac . cm rằng a, aehd là hình chữ nhật b, tam giác abh đồng dạng tam giác ahd c, he^2=ae.ec d, gọi m là giao điểm của be và cd. cm rằng tam giác dbm đồng dạng tam giác ecm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 5 2023
a: góc AEH=góc ADH=góc DAE=90 độ
=>ADHE là hình chữ nhật
b: Xét ΔADH vuông tại D và ΔAHB vuông tại H có
góc DAH chung
=>ΔADH đồng dạng với ΔAHB
c: \(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)
9 tháng 5 2023
a: góc AEH=góc ADH=góc DAE=90 độ
=>AEHD nội tiếp
b: Xét ΔABH vuông tại H và ΔAHD vuông tại D có
góc BAH chung
=>ΔABH đồng dạng với ΔAHD
c: ΔAHC vuông tại H có HE vuông góc AC
nên HE^2=AE*EC
9 tháng 5 2023
a: góc AEH=góc ADH=góc DAE=90 độ
=>ADHE là hình chữ nhật
b: Xét ΔABH vuông tại H và ΔAHD vuông tại D có
góc BAH chung
=>ΔABH đồng dạngvói ΔAHD
c: ΔHAC vuông tại H có HE là đường cao
nên HE^2=AE*EC
CH
Cô Hoàng Huyền
Admin
VIP
28 tháng 2 2018
a) Xét tam giác AHD và tam giác ABH có:
Góc A chung
\(\widehat{ADH}=\widehat{AHB}\left(=90^o\right)\)
\(\Rightarrow\Delta AHD\sim\Delta ABH\left(g-g\right)\)
\(\Rightarrow\frac{AH}{AB}=\frac{AD}{AH}\Rightarrow AH^2=AB.AD\)
b) Ta có tứ giác ADHE có 3 góc vuông nên nó là hình chữ nhật.
Vậy thì \(\widehat{DHA}=\widehat{DEA}\)
Lại có \(\widehat{DHA}=\widehat{CBA}\) nên \(\widehat{DEA}=\widehat{CBA}\)
Suy ra \(\Delta ADE\sim\Delta ACB\left(g-g\right)\)
c) Gọi I là giao điểm của AO và DE.
Xét tam giác vuông ABC có AO là trung tuyến ứng với cạnh huyền nên OA = OC hay \(\widehat{OAC}=\widehat{OCA}\)
Lại có \(\widehat{AED}=\widehat{ABC}\) nên \(\widehat{OAC}+\widehat{DEA}=\widehat{OCA}+\widehat{ABC}=90^o\)
Suy ra \(\widehat{AIE}=90^o\) hay \(AO\perp DE\)
d) Ta có do \(AO\perp DE\) nên:
\(S_{ADOE}=\frac{1}{2}DE.OA=\frac{1}{2}AH.\frac{BC}{2}=\frac{1}{2}a.AH\)
Vậy thì \(S_{ADOE}\) lớn nhất khi AH lớn nhất.
Xét tam giác vuông ABC, ta có
\(BC.AH=AB.AC\le\frac{AB^2+AC^2}{2}=\frac{BC^2}{2}=2a^2\)
\(\Rightarrow AH\le a\)
Vậy AH lớn nhất khi AH = a tức là tam giác ABC vuông cân tại A.
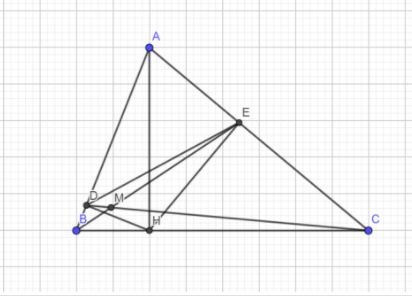
a: góc AEH=góc ADH=góc DAE=90 độ
=>AEHD là hình chữ nhật
b: Xét ΔADH vuông tại D và ΔAHB vuông tại H có
góc DAH chung
=>ΔADH đồng dạng với ΔAHB
c: ΔAHC vuông tại H có HE vuông góc AC
nên HE^2=AE*EC