Giải dùm pương trình này vs ạ
x(-2x+1)=-1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 2 2022
Bài 2:
a: \(\Leftrightarrow4x^2\left(ax-3\right)-\left(ax-3\right)=0\)
\(\Leftrightarrow\left(ax-3\right)\left(2x-1\right)\left(2x+1\right)=0\)
Trường hợp 1: a=0
=>(2x-1)(2x+1)=0
=>x=1/2 hoặc x=-1/2
Trường hợp 2: a<>0
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-\dfrac{1}{2}\\x=\dfrac{3}{a}\end{matrix}\right.\)
b: \(\Leftrightarrow a^2x^2\left(2x+5\right)-4\left(2x+5\right)=0\)
\(\Leftrightarrow\left(2x+5\right)\left(a^2x^2-4\right)=0\)
Trường hợp 1: a=0
Phương trình sẽ là 2x+5=0
hay x=-5/2
Trường hợp 2: a<>0
Phương trình sẽ là \(\left(2x+5\right)\left[\left(ax\right)^2-4\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{5}{2}\\x=-\dfrac{2}{a}\\x=\dfrac{2}{a}\end{matrix}\right.\)
NT
4
12 tháng 2 2017
\(\left(2x+1\right)\left(x+1\right)\left(x-1\right)=4x^2-4x+2x-2\)
\(\Leftrightarrow\left(2x+1\right)\left(x+1\right)\left(x-1\right)=4x\left(x-1\right)+2\left(x-1\right)\)
\(\Leftrightarrow\left(2x+1\right)\left(x+1\right)\left(x-1\right)=\left(x-1\right)\left(4x+2\right)\)
\(\Leftrightarrow\left(2x+1\right)\left(x+1\right)\left(x-1\right)=2\left(x-1\right)\left(2x+1\right)\)
\(\Leftrightarrow\left(2x+1\right)\left(x+1\right)\left(x-1\right)-2\left(x-1\right)\left(2x+1\right)=0\)
\(\Leftrightarrow\left(2x+1\right)\left(x-1\right)\left(x+1-2\right)=0\)
\(\Leftrightarrow\left(2x+1\right)\left(x-1\right)\left(x-1\right)=0\)
\(\orbr{\begin{cases}2x+1=0\\x-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{-1}{2}\\x=1\end{cases}}\)
12 tháng 2 2017
pt\(\Leftrightarrow\left(2x+1\right)\left(x-1\right)\left(x+1\right)=2\left(2x+1\right)\left(x-1\right)\)
\(\Leftrightarrow\left(2x+1\right)\left(x-1\right)\left(x+1-2\right)=0\)
\(\Leftrightarrow\left(2x+1\right)\left(x-1\right)^2=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x+1=0\\x-1=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=-\frac{1}{2}\\x=1\end{cases}}\)
KL vậy....
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
PU
1
13 tháng 7 2016
Ta có : \(x^4-4x=1\Leftrightarrow x^4=4x+1\Leftrightarrow x^4+2x^2+1=2x^2+4x+2\)
\(\Leftrightarrow\left(x^2+1\right)^2=2\left(x+1\right)^2\Leftrightarrow\left(x^2+1\right)^2-2\left(x+1\right)^2=0\)
\(\Leftrightarrow\left[x^2+1-\sqrt{2}\left(x+1\right)\right].\left[x^2+1+\sqrt{2}\left(x+1\right)\right]=0\)
Đến đây thì dễ rồi ^^
19 tháng 11 2023
ĐKXĐ: \(\left\{{}\begin{matrix}2x+5>=0\\4-2x>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x>=-5\\2x< =4\end{matrix}\right.\Leftrightarrow-\dfrac{5}{2}< =x< =2\)
\(x^2+\sqrt{2x+5}+\sqrt{4-2x}=4x-1\)
=>\(x^2-4+\sqrt{2x+5}-3+\sqrt{4-2x}=4x-1-7\)
=>\(\left(x-2\right)\left(x+2\right)+\dfrac{2x+5-9}{\sqrt{2x+5}+3}+\sqrt{4-2x}=4x-8\)
=>\(\left(x-2\right)\left[\left(x+2\right)+\dfrac{2}{\sqrt{2x+5}+3}-4\right]+\sqrt{4-2x}=0\)
=>\(-\left(2-x\right)\left[\left(x-2\right)+\dfrac{2}{\sqrt{2x+5}+3}\right]+\sqrt{2\left(2-x\right)}=0\)
=>\(\sqrt{2-x}\left[-\sqrt{2-x}\left(x-2+\dfrac{2}{\sqrt{2x+5}+3}\right)+\sqrt{2}\right]=0\)
=>\(\sqrt{2-x}=0\)
=>x=2(nhận)
AH
Akai Haruma
Giáo viên
24 tháng 11 2023
Lời giải:
\(P.\frac{1}{\sqrt{2}}=\frac{\sqrt{(x-1)+2\sqrt{x-1}+1}+\sqrt{(x-1)-2\sqrt{x-1}+1}}{\sqrt{(2x-1)+2\sqrt{2x-1}+1}-\sqrt{(2x-1)-2\sqrt{2x-1}+1}}\)
\(=\frac{\sqrt{(\sqrt{x-1}+1)^2}+\sqrt{(\sqrt{x-1}-1)^2}}{\sqrt{(\sqrt{2x-1}+1)^2}-\sqrt{(\sqrt{2x-1}-1)^2}}\)
\(=\frac{\sqrt{x-1}+1+\sqrt{x-1}-1}{\sqrt{2x-1}+1-(\sqrt{2x-1}-1)}=\frac{2\sqrt{x-1}}{2}=\sqrt{x-1}\)
BT
1
9 tháng 4 2018
Lập bảng xét dấu :
| x | \(\frac{-5}{2}\) | \(\frac{1}{3}\) | |||
| 2x+5 | - | 0 | + | \(|\) | + |
| 1-3x | + | \(|\) | + | 0 | - |
+) Nếu \(x\le\frac{-5}{3}\) thì \(|2x+5|=-2x-5\)
\(|1-3x|=1-3x\)
\(pt\Leftrightarrow-2x-5=1-3x\)
\(\Leftrightarrow-2x+3x=1+5\)
\(\Leftrightarrow x=6\)( loại )
+) Nếu \(\frac{-5}{2}< x< \frac{1}{3}\) thì \(|2x+5|=2x+5\)
\(|1-3x|=1-3x\)
\(pt\Leftrightarrow2x+5=1-3x\)
\(\Leftrightarrow2x+3x=1-5\)
\(\Leftrightarrow5x=-4\)
\(\Leftrightarrow x=\frac{-4}{5}\left(tm\right)\)
+) Nếu \(x\ge\frac{1}{3}\) thì \(|2x+5|=2x+5\)
\(|1-3x|=3x-1\)
\(pt\Leftrightarrow2x+5=3x-1\)
\(\Leftrightarrow2x-3x=-1-5\)
\(\Leftrightarrow-x=-6\)
\(\Leftrightarrow x=6\left(tm\right)\)
Vậy ....
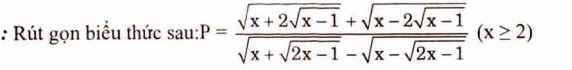
Ta có
\(x\left(-2x+1\right)=-1\)
\(\Rightarrow x=1,-1;\left(-2x+1\right)=1;-1\\ \)
Mà \(\left(-2x+1\right)\le0\\ \left(-2x+1\right)=-1\Leftrightarrow x=1\)
Mik mới lớp 6 nên không chắc lắm