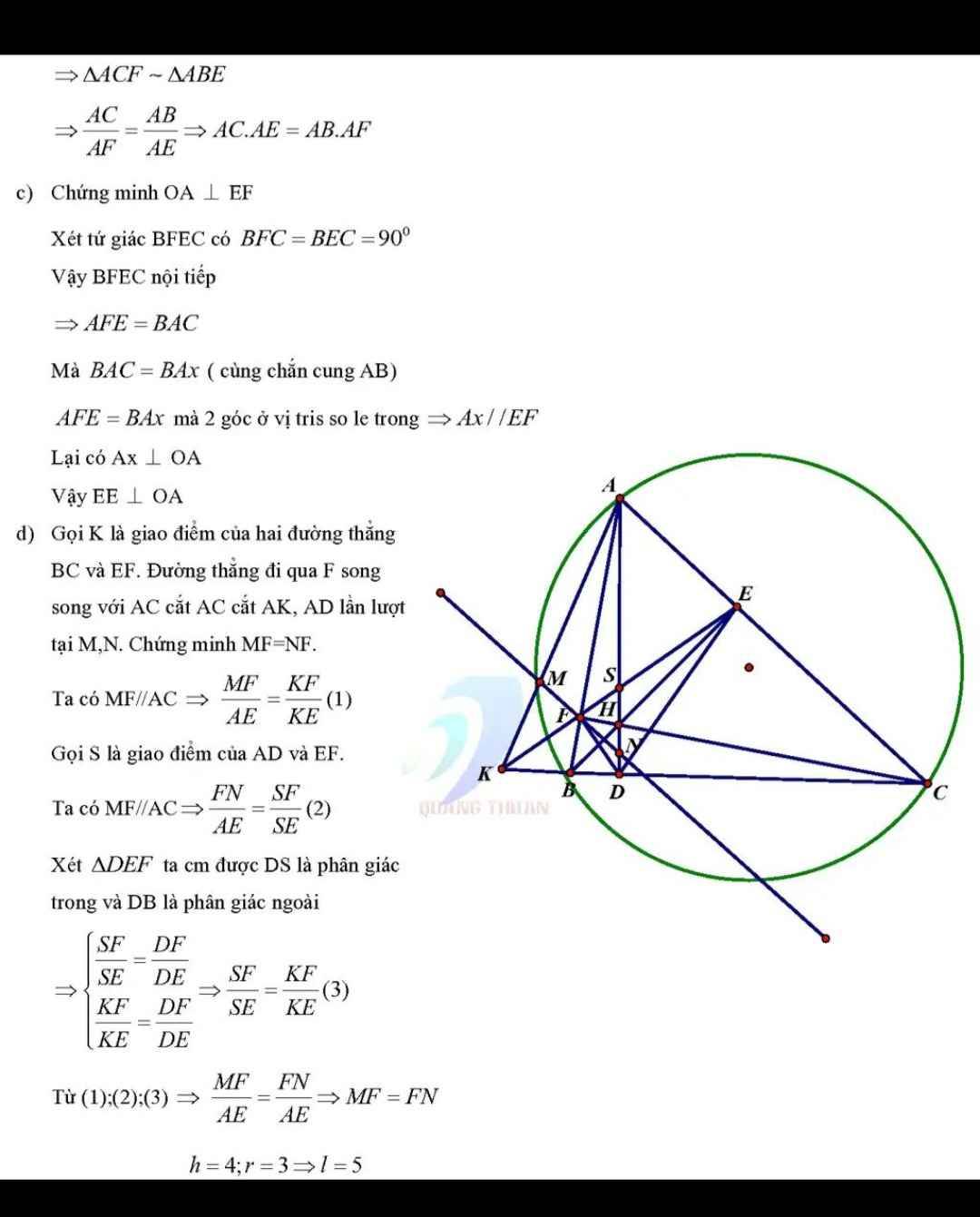
Cho tam giác ABC nhon nội tiếp đ/tr(O), có đường cao AK, BD, CE cắt nhau tại H, tia AK cắt (O) tại Q. N là trung điểm BC, F là trung điểm AH. Kẽ đường kính AG của (O), đường thẳng qua Q song song với ED cắt (O) tại giao điểm thứ 2 là T( T khác Q). Gọi J là giao điểm NF và ED
a) BEDC, và AEHD là các tứ giác nội tiếp.
b) FD vuông góc với ND, suy ra: ND2 = NJ.NF


a: góc BDC=góc BEC=90 độ
=>BEDC nội tiếp
góc AEH+góc ADH=180 độ
=>AEHD nội tiếp