Cho phương trình ( là tham số). Tìm m để phương trình đã cho có hai nghiệm phân biệt
( là tham số). Tìm m để phương trình đã cho có hai nghiệm phân biệt 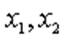 thỏa mãn
thỏa mãn 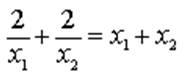
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(1)\) Để m có 2 nghiệm phân biệt thì \(\Delta>0\)
\(\Leftrightarrow\left[-2\left(m+1\right)\right]^2-4\left(m^2+3m+2\right)>0\)
\(\Leftrightarrow4\left(m+1\right)^2-4\left(m^2+3m+2\right)>0\)
\(\Leftrightarrow4\left(m^2+2m+1\right)-4\left(m^2+3m+2\right)>0\)
\(\Leftrightarrow4m^2+8m+4-4m^2-12m-8>0\)
\(\Leftrightarrow-4m-4>0\)
\(\Leftrightarrow-4m>4\)
\(\Leftrightarrow m< -1\)
\(2)\) Theo Vi-ét, ta có :
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+2\\x_1x_2=\dfrac{c}{a}=m^2+3m+2\end{matrix}\right.\)
Ta có :
\(x_1^2+x_2^2=12\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2-12=0\)
\(\Leftrightarrow\left(2m+2\right)^2-2\left(m^2+3m+2\right)-12=0\)
\(\Leftrightarrow4m^2+8m+4-2m^2-6m-4-12=0\)
\(\Leftrightarrow2m^2+2m-12=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=2\\m=-3\end{matrix}\right.\)
m=2 thì phương trình đâu có nghiêm đâu? Phải loại đi chứ

\(\Delta'=1-\left(m-3\right)=4-m>0\Rightarrow m< 4\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m-3\end{matrix}\right.\)
Do \(x_1+x_2=2\Rightarrow x_2=2-x_1\)
Ta có:
\(x_1^2+x_1x_2=2x_2-12\)
\(\Leftrightarrow x_1\left(x_1+x_2\right)=2\left(2-x_1\right)-12\)
\(\Leftrightarrow2x_1=4-2x_1-12\)
\(\Leftrightarrow4x_1=-8\Rightarrow x_1=-2\Rightarrow x_2=4\)
Thế vào \(x_1x_2=m-3\Rightarrow m-3=-8\)
\(\Rightarrow m=-5\)



Lời giải:
Để pt có 2 nghiệm phân biệt thì:
$\Delta'=m^2-(m^2+2m+2)>0$
$\Leftrightarrow 2m+2<0$
$\Leftrightarrow m< -1$
Áp dụng định lý Viet, với $x_1,x_2$ là nghiệm thì:
$x_1+x_2=2m$
$x_1x_2=m^2+2m+2$
$m^2+2m+2=(m+1)^2+1>0$ nên $x_1,x_2$ luôn khác $0$
Khi đó:
$\frac{2}{x_1}+\frac{2}{x_2}=x_1+x_2$
$\Leftrightarrow 2.\frac{x_1+x_2}{x_1x_2}=x_1+x_2$
$\Leftrightarrow 2.\frac{2m}{m^2+2m+2}=2m$
$\Leftrightarrow 2m(\frac{2}{m^2+2m+2}-1)=0$
$\Leftrightarrow m=0$ hoặc $m^2+2m+2=2$
$\Leftrightarrow m=0$ hoặc $m(m+2)=0$
$\Leftrightarrow m=0$ hoặc $m=-2$ Vì $m< -1$ nên $m=-2$