cho hàm số f(x)=căn2x^2+1. Tính giá trị f(-2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 3 2019
a) Ta có:
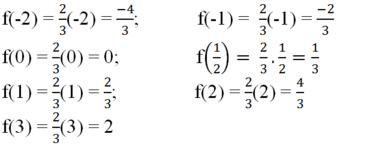
b) Ta có:
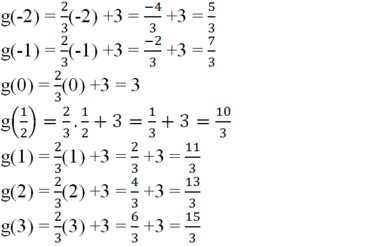
c) Từ kết quả câu a, b ta được bảng sau:
Nhận xét:
- Hai hàm số
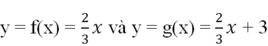
là hai hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng lên.
- Cùng một giá trị của biến x, giá trị của hàm số y = g(x) luôn luôn lớn hơn giá trị tương ứng của hàm số y = f(x) là 3 đơn vị.
6 tháng 12 2021
Giải:
Bài 1: lần lượt thay các giá trị của x, ta có:
_Y=f(-1)= -5.(-1)-1=4
_Y=f(0)= -5.0-1=1
_Y=f(1)= -5.1-1=-6
_Y=f(1/2)= -5.1/2-1=-7/2
6 tháng 12 2021
Bài 2:
Lần lượt thay các giá trị của x, ta có:
_Y=f(-2)=-2.(-2)+3=7
_Y=f(-1)=-2.(-1)+3=1
_Y=f(0)=-2.0+3=3
_Y=f(-1/2)=-2.(-1/2)+3=4
_Y=f(1/2)=-2.1/2+3=2
2 tháng 11 2019
\(f\left(x\right)=\left|x-2015\right|+\left|x+2016\right|\)
a) Ta có: \(\left|x\right|=\orbr{\begin{cases}x=\frac{1}{2}\\x=-\frac{1}{2}\end{cases}}\)
+) Với \(x=\frac{1}{2}\):
\(f\left(\frac{1}{2}\right)=\left|\frac{1}{2}-2015\right|+\left|\frac{1}{2}+2016\right|=2\)
+) Với \(x=-\frac{1}{2}\)
\(f\left(-\frac{1}{2}\right)=\left|-\frac{1}{2}-2015\right|+\left|-\frac{1}{2}+2016\right|=0\)
KN
2 tháng 11 2019
c) Áp dụng BĐT |x| + |y| \(\ge\)|x + y|, ta được:
\(f\left(x\right)=\left|x-2015\right|+\left|x+2016\right|=\left|2015-x\right|+\left|x+2016\right|\)
\(\ge\left|\left(2015-x\right)+\left(x+2016\right)\right|=\left|4031\right|=4031\)
(Dấu "="\(\Leftrightarrow\left(2015-x\right)\left(x+2016\right)\ge0\)
TH1: \(\hept{\begin{cases}2015-x\ge0\\x+2016\ge0\end{cases}}\Leftrightarrow-2016\le x\le2015\)
TH2: \(\hept{\begin{cases}2015-x\le0\\x+2016\le0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge2015\\x\le-2016\end{cases}}\left(L\right)\))
Vậy \(f\left(x\right)_{min}=4031\Leftrightarrow-2016\le x\le2015\)
24 tháng 12 2021
a: f(-3)=10
f(0)=-8
f(1)=-6
f(2)=0
b: f(x)=0
=>(x-2)(x+2)=0
=>x=2 hoặc x=-2
22 tháng 2 2021
Câu 1:
a)
| \(y=f\left(x\right)=2x^2\) | -5 | -3 | 0 | 3 | 5 |
| f(x) | 50 | 18 | 0 | 18 | 50 |
b) Ta có: f(x)=8
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
Vậy: Để f(x)=8 thì \(x\in\left\{2;-2\right\}\)
Ta có: \(f\left(x\right)=6-4\sqrt{2}\)
\(\Leftrightarrow2x^2=6-4\sqrt{2}\)
\(\Leftrightarrow x^2=3-2\sqrt{2}\)
\(\Leftrightarrow x=\sqrt{3-2\sqrt{2}}\)
hay \(x=\sqrt{2}-1\)
Vậy: Để \(f\left(x\right)=6-4\sqrt{2}\) thì \(x=\sqrt{2}-1\)
6 tháng 12 2016
1.
y=f(-1)=3*(-1)-2=-5
y=f(0)=3*0-2=-2
y=f(-2)=3*(-2)-2=-8
y=f(3)=3*3-2=7
Câu 2,3a làm tương tự,chỉ việc thay f(x) thôi.
3b
Khi y=5 =>5=5-2*x=>2*x=0=> x=0
Khi y=3=>3=5-2*x=>2*x=2=>x=1
Khi y=-1=>-1=5-2*x=>2*x=6=>x=3
14 tháng 12 2016
f(-1)=3.1-2=3-2=1
f(0)=3.0-2=0-2=-2
f(-2)=3.(-2)-2=-6-2=-8
f(3)=3.3-2=9-2=7
31 tháng 12 2020
Bài 1:
Thay x=1 vào hàm số \(y=f\left(x\right)=2x^2-5\), ta được:
\(f\left(1\right)=2\cdot1^2-5=2-5=-3\)
Thay x=-2 vào hàm số \(y=f\left(x\right)=2x^2-5\), ta được:
\(f\left(-2\right)=2\cdot\left(-2\right)^2-5=2\cdot4-5=3\)
Thay x=0 vào hàm số \(y=f\left(x\right)=2x^2-5\), ta được:
\(f\left(0\right)=2\cdot0^2-5=-5\)
Thay x=2 vào hàm số \(y=f\left(x\right)=2x^2-5\), ta được:
\(f\left(2\right)=2\cdot2^2-5=8-5=3\)
Thay \(x=\dfrac{1}{2}\) vào hàm số \(y=f\left(x\right)=2x^2-5\), ta được:
\(f\left(\dfrac{1}{2}\right)=2\cdot\left(\dfrac{1}{2}\right)^2-5=2\cdot\dfrac{1}{4}-5=-\dfrac{9}{2}\)
Vậy: f(1)=-3; f(-2)=3; f(0)=-5; f(2)=3; \(f\left(\dfrac{1}{2}\right)=-\dfrac{9}{2}\)
AH
Akai Haruma
Giáo viên
31 tháng 12 2020
Bài 1:
\(f(x)=2x^2-5\) thì:
$f(1)=2.1^2-5=-3$
$f(-2)=2(-2)^2-5=3$
$f(0)=2.0^2-5=-5$
$f(2)=2.2^2-5=3$
$f(\frac{1}{2})=2(\frac{1}{2})^2-5=\frac{-9}{2}$
f(x)=\(\sqrt{2x^2+1}\)
Khi đó: f(-2)=\(\sqrt{2.\left(-2\right)^2+1}\)=\(\sqrt{9}\)=3