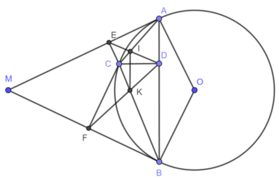
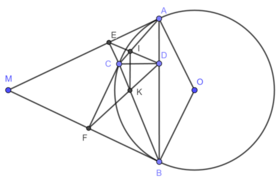
Cho tam giác đều ABC nội tiếp đường tròn O. Trên cung nhỏ BC lấy điểm M ( M khác B,C), gọi D là giao điểm của MA và BC. Từ D kẻ DE,DF lần lượt vuông góc với các cạnh AB và AC
a. cm AEDF nội tiếp
b.gọi h là trung điểm BC.cm HE=HF
c.1phần MD= 1 phần MB + 1 phần MC



a)Trên tia MA lấy điểm I sao cho MI=MC
Dễ thấy ΔCIMΔCIM đều ⇒MC=CI⇒MC=CI
Xét 2 tam giác ΔAICΔAICvàΔBMCvàΔBMC có
IC=MCIC=MC
∠IAC=∠MCB∠IAC=∠MCB (vì cùng cộng với ∠BCI=60∘∠BCI=60∘)
AC=BCAC=BC
Do đó ΔAICΔAIC = ΔBMCΔBMC
⇒AI=BM⇒AI=BM
⇒⇒ Đpcm
b) Dễ thấy ΔBAM∼ΔDCMΔBAM∼ΔDCM(g.g)
nên AMCM=BMDM⇒AM.DM=CM.BMAMCM=BMDM⇒AM.DM=CM.BM
⇒AMBM.CM=1MD⇒AMBM.CM=1MD
Áp dụng kết quả câu (a) ta có đpcm
c) Đặt MA=x, MB=y. Ta có
AM2+BM2+CM2=x2+y2+(x−y)2=2(x2+y2−xy)AM2+BM2+CM2=x2+y2+(x−y)2=2(x2+y2−xy) (1)
Kẻ BHBH vuông góc với AMAM
Do ∠BMH=60∘∠BMH=60∘ nên MH=y2,BH2=y2−(y2)2=3y24MH=y2,BH2=y2−(y2)2=3y24
do đó AB2=AH2+BH2=x2+y2−xyAB2=AH2+BH2=x2+y2−xy (2)
Từ (1) và (2) ⇒MA2+MB2+MC2=2AB2⇒MA2+MB2+MC2=2AB2 mà ΔABCΔABC đều
nên AB=R√3
k cho mình nha!!