phương trình chứa ẩn ở mẫu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 3 2021
Phương trình chứa ẩn ở mẫu thì phải có ĐKXĐ để mẫu khác 0, và phải khử mẫu và còn phải loại những giá trị không thỏa mãn ĐK
Phương trình không chứa ẩn ở mẫu thì chỉ cần giải phương trình như bình thường
YN
19 tháng 2 2022
Answer:
e) \(\frac{x-3}{x-2}-\frac{x-2}{x-4}=3\frac{1}{5}\left(ĐK:x\ne2;x\ne4\right)\)
\(\Leftrightarrow\frac{\left(x-3\right)\left(x-4\right)-\left(x-2\right)\left(x-2\right)}{\left(x-2\right)\left(x-4\right)}=\frac{16}{5}\)
\(\Leftrightarrow x^2-7x+12-x^2+4x-4=\frac{16}{5}.\left(x-2\right)\left(x-4\right)\)
\(\Leftrightarrow-3x+8=\frac{16}{5}.\left(x^2-6x+8\right)\)
\(\Leftrightarrow-3x+8=\frac{16}{5}x^2-\frac{96}{5}x+\frac{128}{5}\)
\(\Leftrightarrow-\frac{16}{5}x^2+\frac{81}{5}x-\frac{88}{5}=0\)
\(\Leftrightarrow-\frac{16}{5}.\left(x^2-\frac{81}{16}x+\frac{11}{2}\right)=0\)
\(\Leftrightarrow x^2-\frac{81}{16}x+\frac{6561}{1024}-\frac{929}{1024}=0\)
\(\Leftrightarrow\left(x-\frac{81}{32}\right)^2=\frac{929}{1024}\)
\(\Leftrightarrow\orbr{\begin{cases}x-\frac{81}{32}=\frac{\sqrt{929}}{32}\\x-\frac{81}{32}=-\frac{\sqrt{929}}{32}\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{81+\sqrt{929}}{32}\\x=\frac{81-\sqrt{929}}{32}\end{cases}}}\)
f) \(\frac{x-3}{x-2}+\frac{x-2}{x-4}=-1\left(ĐK:x\ne2;x\ne4\right)\)
\(\Leftrightarrow\frac{\left(x-3\right)\left(x-4\right)+\left(x-2\right)\left(x-2\right)}{\left(x-2\right)\left(x-4\right)}=\frac{-\left(x-2\right)\left(x-4\right)}{\left(x-2\right)\left(x-4\right)}\)
\(\Leftrightarrow x^2-4x-3x+12+x^2-4x+4=-x^2+4x+2x-8\)
\(\Leftrightarrow x^2+x^2+x^2-4x-3x-4x-4x-2x+12+4+8=0\)
\(\Leftrightarrow3x^2-9x-8x+24=0\)
\(\Leftrightarrow3x\left(x-3\right)-8\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(3x-8\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\\3x-8=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=3\\x=\frac{8}{3}\end{cases}}}\)
13 tháng 9 2023
a: ĐKXĐ: x<>1
\(PT\Leftrightarrow1+\dfrac{1}{x-1}+\dfrac{x}{\left(x-1\right)^2}=0\)
=>\(\dfrac{\left(x-1\right)^2+x-1+x}{\left(x-1\right)^2}=0\)
=>x^2-2x+1+2x-1=0
=>x^2=0
=>x=0
b: ĐKXĐ: x<>1
Đề sai rồi bạn, sao lại có hai dấu bằng kìa
18 tháng 2 2022
a, ĐKXĐ:\(\left\{{}\begin{matrix}x+4\ne0\\x-1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-4\\x\ne1\end{matrix}\right.\)
b, ĐKXĐ:\(\left\{{}\begin{matrix}5\left(x-2\right)\ne0\\3\left(x+2\right)\ne0\\x^2-4\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne2\\x\ne-2\\x\ne\pm2\end{matrix}\right.\Leftrightarrow x\ne\pm2\)
c, ĐKXĐ:\(\left\{{}\begin{matrix}4x^2-8x+7\ne0\\4x^2-10x+7\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4\left(x^2-2x+\dfrac{7}{4}\right)\ne0\\4\left(x^2-\dfrac{10}{4}x+\dfrac{7}{4}\right)\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x^2-2x+1\right)+\dfrac{3}{4}\ne0\\\left(x^2-2.\dfrac{10}{8}.x+\dfrac{25}{16}\right)+\dfrac{3}{16}\ne0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)^2+\dfrac{3}{4}\ne0\left(luôn.đúng\right)\\\left(x-\dfrac{5}{4}\right)^2+\dfrac{3}{16}\ne0\left(luôn.đúng\right)\end{matrix}\right.\)
\(\Leftrightarrow x\in R\)
18 tháng 2 2022
a, đkxđ \(\left\{{}\begin{matrix}x+4\ne0\\x-1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-4\\x\ne1\end{matrix}\right.\)
b, đkxđ \(\left\{{}\begin{matrix}x-2\ne0\\x+2\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne2\\x\ne-2\end{matrix}\right.\)
c, đkxđ \(\left\{{}\begin{matrix}4x^2-8x+7\ne0\\4x^2-10x+7\ne0\end{matrix}\right.\)*luôn đúng *
Vậy \(x\in R\)
H9
HT.Phong (9A5)
CTVHS
15 tháng 2 2023
\(\dfrac{5}{3x+2}=2x-1\)
\(\Leftrightarrow\dfrac{5}{3x+2}=\dfrac{\left(3x+2\right)\left(2x-1\right)}{3x+2}\)
\(\Leftrightarrow5=\left(3x+2\right)\left(2x-1\right)\)
\(\Leftrightarrow5=6x^2-3x+4x-2\)
\(\Leftrightarrow5=6x^2+x-2\)
\(\Leftrightarrow6x^2+x=7\)
\(\Leftrightarrow x=1\)
PT
1
CM
10 tháng 9 2017
Khi giải phương trình chứa ẩn ở mẫu, ta phải chú ý đến điều kiện xác định của phương trình.
TD
2
0
29 tháng 3 2018
1. Điều kiện xác định của một phương trình
Điều kiện xác định của phương trình là tập hợp các giá trị của ẩn làm cho tất cả các mẫu trong phương trình đều khác 0. Điều kiện xác định của phương trình viết tắt là ĐKXĐ.
2. Giải phương trình chứa ẩn số ở mẫu
Ta thường qua các bước:
Bước 1: Tìm điều kiện xác của phương trình
Bước 2: Quy đồng mẫu hai vế rồi khử mẫu.
Bước 3: Giải phương trình tìm được.
Bước 4: Kết luận.
Nghiệm của phương trình là giá trị của ẩn thoả mãn ĐKXĐ của phương trình.
29 tháng 3 2018
1. Điều kiện xác định của một phương trình
Điều kiện xác định của phương trình là tập hợp các giá trị của ẩn làm cho tất cả các mẫu trong phương trình đều khác 0. Điều kiện xác định của phương trình viết tắt là ĐKXĐ.
2. Giải phương trình chứa ẩn số ở mẫu
Ta thường qua các bước:
Bước 1: Tìm điều kiện xác của phương trình
Bước 2: Quy đồng mẫu hai vế rồi khử mẫu.
Bước 3: Giải phương trình tìm được.
Bước 4: Kết luận.
Nghiệm của phương trình là giá trị của ẩn thoả mãn ĐKXĐ của phương trình.
LD
1
24 tháng 2 2022
ĐKXĐ:\(x\ne-3\)
\(-\dfrac{4}{3+x}+5=\dfrac{4x+7}{x+3}\\ \Leftrightarrow\dfrac{-4}{x+3}+\dfrac{5\left(x+3\right)}{x+3}-\dfrac{4x+7}{x+3}=0\\ \Leftrightarrow\dfrac{-4+5x+15-4x-7}{x+3}=0\\ \Rightarrow x+4=0\\ \Leftrightarrow x=-4\left(tm\right)\)
PT
1
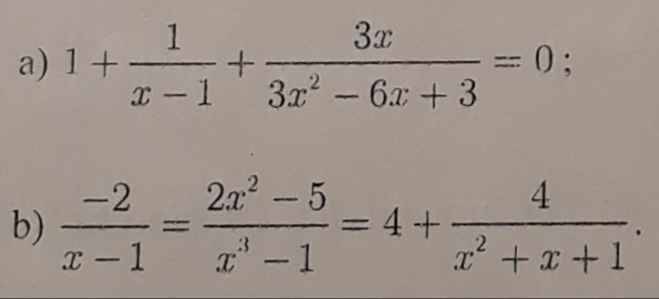
Đề thiếu phương trình. Bạn xem lại.