Hai dây dẫn thẳng song song dài vô hạn đặt cách nhau 8 cm trong không khí. Dòng điện chạy trong hai dây là I1 = 10A, I2 = 20A và ngược chiều nhau. Tìm cảm ứng từ tại điểm cách mỗi dây 5 cm. Có thể giải thích cho mik cách cụ thể để tìm góc alpha được ko> Mình cảm ơn ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cảm ứng tại M:
\(B_1=2\pi\cdot10^{-7}\cdot\dfrac{I_1}{r_1}=2\pi\cdot10^{-7}\cdot\dfrac{10}{0,04}=1,57\cdot10^{-4}T\)
\(B_2=2\pi\cdot10^{-7}\cdot\dfrac{I_2}{r_2}=2\pi\cdot10^{-7}\cdot\dfrac{20}{0,14}=8,98\cdot10^{-5}T\)
Hai dây dẫn ngược chiều nhau:
\(B_M=B_1-B_2=1,57\cdot10^{-4}-8,98\cdot10^{-5}=6,72\cdot10^{-5}T\)

\(B_1=\dfrac{I_1}{r}.2.10^{-7}\left(T\right)=B_2\)
\(\Rightarrow\sum B=B_1+B_2+2B_1B_2\cos60^0=...\left(T\right)\)

a)Hai dây cùng chiều:
\(B_1=2\cdot10^{-7}\cdot\dfrac{I_1}{r_1}=2\cdot10^{-7}\cdot\dfrac{10}{0,02}=1\cdot10^{-4}T\)
\(B_2=2\cdot10^{-7}\cdot\dfrac{I_2}{r_2}=2\cdot10^{-7}\cdot\dfrac{20}{0,02}=2\cdot10^{-4}T\)
\(B=B_1+B_2=1\cdot10^{-4}+2\cdot10^{-4}=3\cdot10^{-4}T\)
b)Hai dây dẫn ngược chiều nhau.
\(B_1=2\cdot10^{-7}\cdot\dfrac{I_1}{r_1}=2\cdot10^{-7}\cdot\dfrac{10}{0,06}=3,33\cdot10^{-5}T\)
\(B_2=2\cdot10^{-7}\cdot\dfrac{I_2}{r_2}=2\cdot10^{-7}\cdot\dfrac{20}{0,02}=2\cdot10^{-4}T\)
\(B=\left|B_1-B_2\right|=\left|3,33\cdot10^{-5}-2\cdot10^{-4}\right|=1,667\cdot10^{-4}T\)

Chọn B
Điểm B cách dây 1 đoạn 4cm cách dây 2 đoạn 14cm
+ Điểm B thỏa mãn đề bài sẽ nằm ngoài đoạn nối 2 dây và gần dây 1 hơn
+ Cảm ứng từ tại B thỏa mãn B → = B → 1 + B → 2 , dựa vào hình vẽ ta có B → 1 ↑ ↓ B → 2
→ B = B 1 − B 2 = 2.10 − 7 . 10 0 , 04 − 20 0 , 14 = 2 , 143.10 − 5 T

Đáp án B
Cảm ứng từ do I 1 gây ra tại M là B 1 = 2 .10 − 7 . 5 0 , 1 = 10 − 5 T .
Cảm ứng từ do I 2 gây ra tại M là B 2 = 2 .10 − 7 . 5 0 , 1 = 10 − 5 T .
Do I 1 , I 2 và M lập thành tam giác đều nên I 1 MI 2 ^ bằng 60 o , suy ra góc giữa B 1 ^ và B 2 ^ bằng 120 o
Ta có: B 2 = B 1 2 + B 2 2 + 2 . B 1 . B 2 . cos 120 ° = 10 − 5 T .


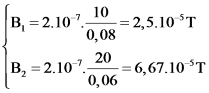 + Thay số ta được
+ Thay số ta được
\(B_1=2.10^{-7}.\dfrac{I_1}{R_1}=2.10^{-7}.\dfrac{10}{0,05}=4.10^{-5}T\)
\(B_2=2.10^{-7}.\dfrac{I_2}{R_2}=2.10^{-7}.\dfrac{20}{0,05}=8.10^{-5}T\)
\(\overrightarrow{B}=B_1+B_2=4.10^{-5}+8.10^{-5}=1,2.10^{-4}T\)