Khai triển đa thức (x+5)4 + (x-5)4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\begin{array}{l}{(x - 3)^4} = {x^4} + 4{x^3}.( - 3) + 6{x^2}.{( - 3)^2} + 4x.{( - 3)^3} + {( - 3)^4}\\ = {x^4} - 12{x^3} + 54{x^2} - 108x + 81\end{array}\)
b) \({(3x - 2y)^4} = 81{x^4} - 216{x^3}y + 216{x^2}{y^2} - 96x{y^3} + 16{y^4}\)
c)
\(\begin{array}{l}{(x + 5)^4} + {(x - 5)^4} = {x^4} + 20{x^3} + 150{x^2} + 500x + 625\\ + {x^4} - 20{x^3} + 150{x^2} - 500x + 625\\ = 2{x^4} + 300{x^2} + 1250\end{array}\)
d) \({(x - 2y)^5} = {x^5} - 10{x^4}y + 40{x^3}{y^2} - 80{x^2}{y^3} + 80x{y^4} - 32{y^5}\)

\(A=\left(2x\right)^4+4.\left(2x\right)^3.1+6\left(2x\right)^2.1+4.\left(2x\right).1+1+3^5+5.3^4.x+10.3^3.x^2+10.3^2.x^3+5.3.x^4+x^5\)
\(A=16x^4+32x^3+24x^2+8x+1+243+405x+270x^2+90x^3+15x^4+x^5\)
\(A=x^5+31x^4+122x^3+294x^2+413x+244\)


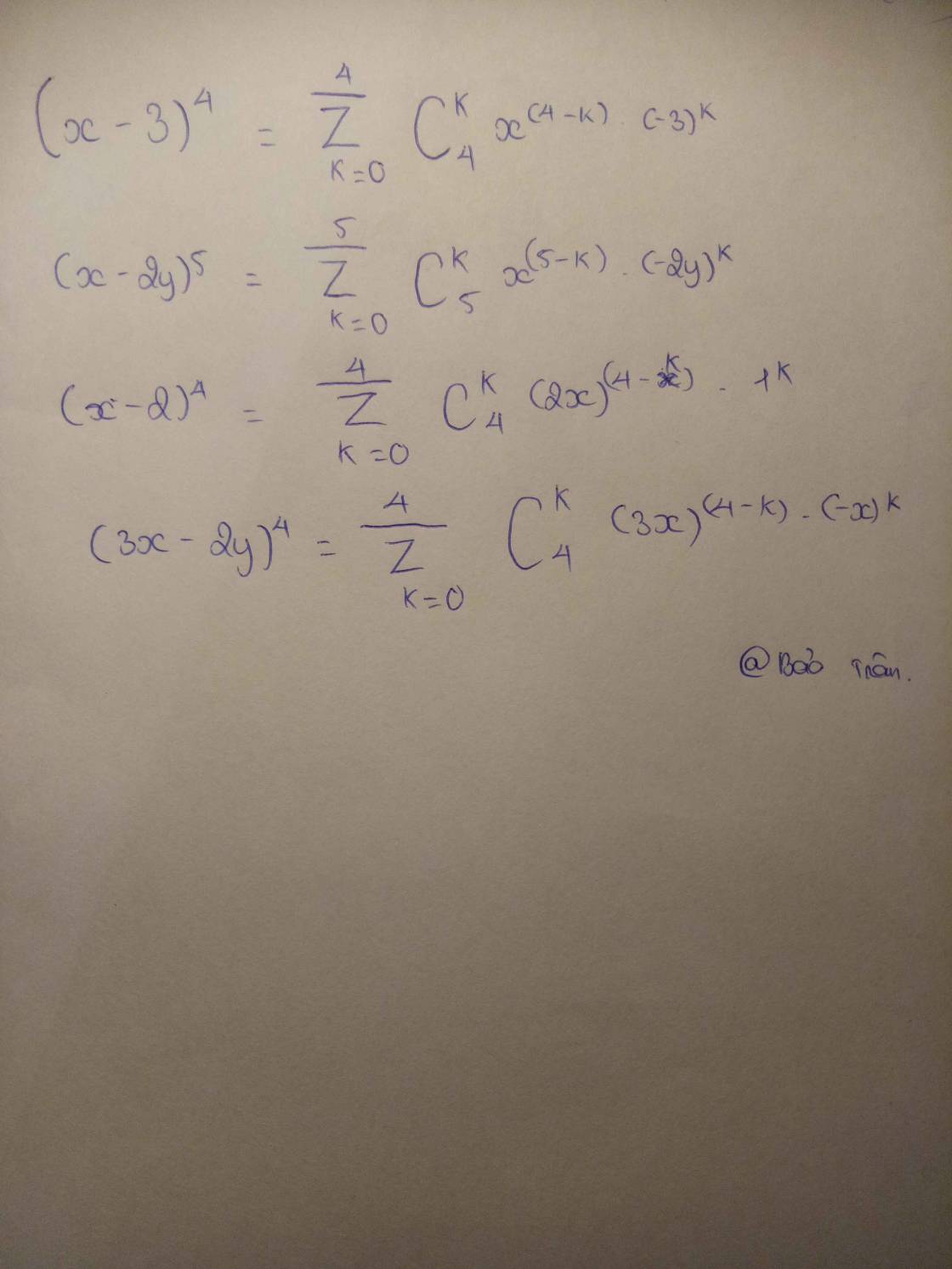

\(\left(x+5\right)^4+\left(x-5\right)^4=\left[\left(x+5\right)^4+2.\left(x+5\right)^2.\left(x-5\right)+\left(x-5\right)^4\right]-2.\left(x+5\right)^2\left(x-5\right)^2\)
\(=\left[\left(x+5\right)^2-\left(x-5\right)^2\right]^2-\left[\sqrt{2}\left(x+5\right)\left(x-5\right)\right]^2\)
\(=\left[\left(x+5\right)^2+\left(x-5\right)^2+\sqrt{2}\left(x+5\right)\left(x-5\right)\right]^2\)
Sau đó bạn áp dụng hằng đẳng thức thứ nhất và thứ 2 ( bình phương 1 tổng và bình phương 1 hiệu tính ra nhé