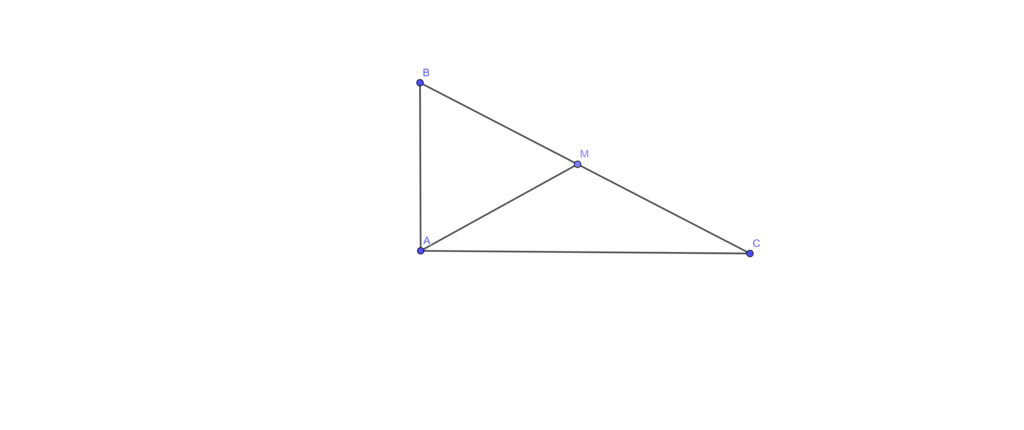
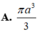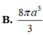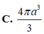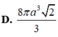Cho tam giác ABCvuông tại A (AB<AC) ,phân giác AD (D thuộc BC) .Trên cạnh AC lấy điểm E sao cho AE=AB
a) Chứng minh : BD=ED
b) Gọi K là giao điểm của các đường thẳng AB và ED .Chứng minh : tam giác BDK=tam giác EDC
c) Tính độ dài CK ,biết AC=\(\sqrt{5}\)