2x2-(m+1)x+m-1=0
Tìm các giá trị của m để hiệu 2 nghiệm bằng tích của chúng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 5 2023
Sửa đề: Có tổng 2 nghiệm bằng tích của chúng
Δ=(m+1)^2-4*2*(m-1)
=m^2+2m+1-8m+8=m^2-6m+9=(m-3)^2>=0
=>Phương trình luôn có hai nghiệm
x1+x2=x1*x2
=>(m+1)/2=(m-1)/2
=>m=0
LD
15 tháng 5 2023
Sửa đề: Có tổng 2 nghiệm bằng tích của chúng
Δ=(m+1)^2-4*2*(m-1)
=m^2+2m+1-8m+8=m^2-6m+9=(m-3)^2>=0
=>Phương trình luôn có hai nghiệm
x1+x2=x1*x2
=>(m+1)/2=(m-1)/2
=>m=0
KV
17 tháng 5 2023
∆ = m² - 4(m - 5)
= m² - 4m + 5
= (m² - 4m + 4) + 1
= (m - 2)² + 1 > 0 với mọi m
Phương trình luôn có 2 nghiệm phân biệt
Theo Viét ta có:
x₁ + x₂ = m (1)
x₁.x₂ = m - 5 (2)
x₁ + 2x₂ = 1 (3)
Lấy (3) - (1) ta được x₂ = 1 - m thay vào (1) ta được
x₁ + 1 - m = m
⇔ x₁ = 2m - 1
Thay x₁ = 2m - 1 và x₂ = 1 - m vào (2) ta được:
(2m - 1)(1 - m) = m - 5
⇔ 2m - 2m² - 1 + m - m + 5 = 0
⇔ -2m² + 2m + 5 = 0
∆ = 4 - 4.(-2).5
= 44
m₁ = -1 + √11
m₂ = -1 - √11
Vậy m = -1 + √11; m = -1 - √11 thì phương trình đã cho có hai nghiệm thỏa mãn x₁ + 2x₂ = 1
KV
10 tháng 5 2021
\(\left(2x+m\right)\left(x-1\right)-2x^2+mx+m-2=0\)
\(\Leftrightarrow2x^2-2x+mx-m-2x^2+mx+m-2=0\)
\(\Leftrightarrow\left(2m-2\right)x-2=0\)
\(\Leftrightarrow\left(2m-2\right)x=2\)
\(\Leftrightarrow x=\dfrac{2}{2m-2}\)
Để phương trình đã cho có nghiệm âm thì:
\(\dfrac{2}{2m-2}< 0\)
\(\Leftrightarrow2m-2< 0\)
\(\Leftrightarrow2m< 2\)
\(\Leftrightarrow m< 1\)
Vậy \(m< 1\) thì phương trình đã cho có nghiệm âm.
DK
10 tháng 5 2021
\(\left(2x+m\right)\left(x-1\right)-2x^2+mx+m-2=0\)
\(\Leftrightarrow2x^2+mx-2x-m-2x^2+mx+m-2=0\)
\(\Leftrightarrow\left(2m-2\right)x-2=0\left(1\right)\)
+) Nếu \(m=1\)\(\rightarrow\left(1\right)\Leftrightarrow0x-2=0\left(V_{n_o}\right)\)
+) Nếu \(m\ne1\rightarrow x=\dfrac{2}{2m-2}\)
Để \(x< 0\Leftrightarrow\dfrac{2}{2m-2}< 0\) mà \(2>0\Leftrightarrow2m-2< 0\Leftrightarrow m< 1\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2022
Phương trình có nghiệm khi:
\(\Delta'=\left(m+1\right)^2-\left(m^2+m+1\right)\ge0\)
\(\Rightarrow m\ge0\)
Khi đó: \(\left\{{}\begin{matrix}x_1=m+1-\sqrt{m}\\x_2=m+1+\sqrt{m}\end{matrix}\right.\)
17 tháng 2 2022
\(\left\{{}\begin{matrix}x+my=3\\x+2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m-2\right)y=2\\x=1-2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{2}{m-2}\\x=1-\dfrac{4}{m-2}=\dfrac{m-6}{m-2}\end{matrix}\right.\)
a, Ta có x < 0 ; y > 0
\(x< 0\Rightarrow\dfrac{m-6}{m-2}< 0\)
Ta có : m - 2 > m - 6
\(\left\{{}\begin{matrix}m-2>0\\m-6< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>2\\m< 6\end{matrix}\right.\Leftrightarrow2< m< 6\)
\(y>0\Leftrightarrow\dfrac{2}{m-2}>0\Rightarrow m>2\)
Vậy 2 < m < 6
b, \(x-2y=3\Rightarrow\dfrac{m-6}{m-2}-\dfrac{4}{m-2}=3\Leftrightarrow\dfrac{m-10}{m-2}=3\)
\(\Rightarrow m-10=3m-6\Leftrightarrow2m=-4\Leftrightarrow m=-2\)
2
13 tháng 1 2023
Ptr có: `\Delta'=[-(m-1)^2]+4m=m^2-2m+1+4m=(m+1)^2 >= 0`
`=>{(x_1+x_2=[-b]/a=2m-2),(x_1.x_2=c/a=-4m):}`
Để ptr có ít nhất `1` nghiệm không âm
`<=>2` nghiệm đều `>= 0`, hoặc có duy nhất `1` nghiệm và `>= 0` hoặc `1` nghiệm `>= 0` và `1` nghiệm `< 0`
`@TH1: 2` nghiệm đều `>= 0`
`=>{(x_1.x_2 >= 0),(x_1+x_2 >= 0):}`
`<=>{(-4m >= 0),(2m-2 >= 0):}`
`<=>{(m <= 0),(m >= 1):}=>` Không có `m` t/m
`@TH2:` Có duy nhất `1` nghiệm và nghiệm đó `>= 0`
`=>{((m+1)^2=0),(x=[-b']/a):}`
`<=>{(m=-1),(x=m-1):}`
`<=>{(m=-1),(x=-2):}` (ko t/m `x >= 0`)
`@TH3:` Có `2` nghiệm pb có `1` nghiệm `< 0` và `1` nghiệm `>= 0`
`=>{(m+1 \ne 0),(x_1.x_2 < 0):}`
`<=>{(m \ne -1),(-4m < 0):}`
`<=>{(m \ne -1),(m > 0):}`
`<=>m > 0`
Vậy `m > 0` thì ptr đã cho có ít nhất `1` nghiệm không âm.
A
8 tháng 6 2023
a) Để phương trình có 2 nghiệm phân biệt
<=> \(\Delta=\left[-\left(4m+3\right)^2\right]-4.2.\left(2m-1\right)=16m^2+24m+9-16m+8=16m^2+8m+1+16=\left(4m+1\right)^2+16>0\)
với mọi giá trị của m.
Vậy phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m.
b) Vì phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m nên ta có: x1+x2= \(\dfrac{4m+3}{2}\)và x1.x2=\(\dfrac{2m-1}{2}\)
31 tháng 3 2023
x1+x2=2m+2; x1x2=m^2+4
x1^2+2(m+1)x2<=2m^2+20
=>x1^2+x2(x1+x2)<=2m^2+20
=>x1^2+x2x1+x2^2<=2m^2+20
=>(x1+x2)^2-x1x2<=2m^2+20
=>(2m+2)^2-(m^2+4)<=2m^2+20
=>4m^2+8m+4-m^2-4-2m^2-20<=0
=>m^2-8m-20<=0
=>m<=-10 hoặc m>2
LD
31 tháng 3 2023
\(x^2-2\left(m+1\right)x+m^2+4=0\left(1\right)\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta'>0\) hay \(\Delta'=\left(m+1\right)^2-m^2-4=m^2+2m+1-m^2-4=2m-4>0\Leftrightarrow m>2\)
Theo hệ thức Viét ta có : \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1.x_2=m^2+4\end{matrix}\right.\)
Vì \(x_1^2\) là nghiệm của phương trình (1) nên ta có : \(x_1^2-2\left(m+1\right)x+m^2+4=0\Leftrightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)
Ta lại có : \(x_1^2+2\left(m+1\right)x_2\le2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2\le2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)-m^2-4\le2m^2+20\)
\(\Leftrightarrow4\left(m+1\right)^2-m^2\le2m^2+20\)
\(\Leftrightarrow4\left(m^2+2m+1\right)-m^2\le2m^2+20\)
\(\Leftrightarrow m^2+8m-16\le0\)
\(\Leftrightarrow-10\le m\le2\)
Kết hợp điều kiện....
CM
11 tháng 11 2018
a) Xét: x2 - 4mx + 9.(m – 1)2 = 0 (1)
Δ’ = (2.m)2 – 9.(m – 1)2 = 4m2 – 9.(m2 – 2m + 1) = -5m2 + 18m – 9
Phương trình (1) có nghiệm ⇔ Δ’ ≥ 0
⇔ -5m2 + 18m – 9 ≥ 0
⇔ 5m2 - 18m + 9 ≤ 0
⇔ (5m – 3)(m – 3) ≤ 0
⇔ 3/5 ≤ m ≤ 3.
b) + x1 ; x2 là hai nghiệm của (1) nên theo định lý Vi-et ta có:
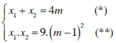
+ Tìm hệ thức giữa x1 và x2 không phụ thuộc vào m.
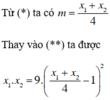
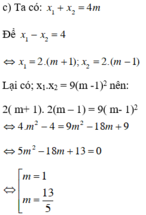
Thử lại:
+ m = 1, (1) trở thành x2 – 4x = 0 có hai nghiệm x = 0; x = 4 có hiệu bằng 4
+ m = 13/5, (1) trở thành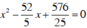 
có hai nghiệm x = 7,2 và x = 3,2 có hiệu bằng 4.
Vậy m = 1 hoặc m = 13/5.
\(2x^2-\left(m+1\right)x+m-1=0\left(1\right)\)
Để phương trình (1) có nghiệm thì:
\(\Delta\ge0\Rightarrow\left(m+1\right)^2-4.2.\left(m-1\right)\ge0\)
\(\Leftrightarrow m^2+2m+1-8m+8\ge0\)
\(\Leftrightarrow\left(m-3\right)^2\ge0\) (luôn đúng)
Vậy \(\forall m\) thì phương trình (1) luôn có nghiệm.
Giả sử phương trình (1) có 2 nghiệm x1, x2 với \(x_1\ge x_2\) \(\Rightarrow x_1-x_2\ge0\)
Theo định lí Viete ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{m+1}{2}\\x_1x_2=\dfrac{m-1}{2}\end{matrix}\right.\)
Vì hiệu 2 nghiệm bằng tích của chúng nên ta có:
\(x_1-x_2=\left|x_1x_2\right|\)
\(\Leftrightarrow\left(x_1-x_2\right)^2=\left(x_1x_2\right)^2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=\left(x_1x_2\right)^2\)
\(\Leftrightarrow\left(\dfrac{m+1}{2}\right)^2-4.\dfrac{m-1}{2}=\left(\dfrac{m-1}{2}\right)^2\)
\(\Leftrightarrow\left(m+1\right)^2-8\left(m-1\right)=\left(m-1\right)^2\)
\(\Leftrightarrow m^2+2m+1-8m+8=m^2-2m+1\)
\(\Leftrightarrow4m=8\Leftrightarrow m=2\)
Vậy \(m=2\)
x1-x2=(m-1)/2
=>(x1-x2)^2=(m-1)^2/4
=>(x1+x2)^2-4x1x2=1/4(m^2-2m+1)
=>(m+1/2)^2-4*(m-1)/2=1/4m^2-1/2m+1/4
=>m^2+m+1/4-2m+2-1/4m^2+1/2m-1/4=0
=>3/4m^2-1/2m+2=0
=>3m^2-2m+8=0
=>PTVN