Pt 2x^2-3x-4=0 A= (1/x1)^2+(1/x2)^2 giúp tớ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^2-2x-\sqrt{3}+1=0\)
\(\Delta'=1^2+\sqrt{3}-1=\sqrt{3}>0\)
⇒ Phương trình có hai nghiệm phân biệt
Theo Viét : \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1.x_2=1-\sqrt{3}\end{matrix}\right.\)
Ta có : \(A=x_1^2.x_2^2-2x_1x_2-x_1-x_2\)
\(=\left(x_1x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)\)
\(=\left(1-\sqrt{3}\right)^2-2\left(1-\sqrt{3}\right)-2=4-2\sqrt{3}-2+2\sqrt{3}-2=0\)
Vậy....
cho PT 2x^2-3x-1=0. x1, x2 là 2 nghiệm của PT, không giải PT hãy tính A = x1^4 + x2^4. B = I x1-x2 I


1.
Đặt \(x^2-2x+m=t\), phương trình trở thành \(t^2-2t+m=x\)
Ta có hệ \(\left\{{}\begin{matrix}x^2-2x+m=t\\t^2-2t+m=x\end{matrix}\right.\)
\(\Rightarrow\left(x-t\right)\left(x+t-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=t\\x=1-t\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=x^2-2x+m\\x=1-x^2+2x-m\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-x^2+3x\\m=-x^2+x+1\end{matrix}\right.\)
Phương trình hoành độ giao điểm của \(y=-x^2+x+1\) và \(y=-x^2+3x\):
\(-x^2+x+1=-x^2+3x\)
\(\Leftrightarrow x=\dfrac{1}{2}\Rightarrow y=\dfrac{5}{4}\)
Đồ thị hàm số \(y=-x^2+3x\) và \(y=-x^2+x+1\):
Dựa vào đồ thị, yêu cầu bài toán thỏa mãn khi \(m< \dfrac{5}{4}\)
Mà \(m\in\left[-10;10\right]\Rightarrow m\in[-10;\dfrac{5}{4})\)
Có cách nào lm bài này bằng cách lập bảng biến thiên k ạ

theo đề bài ta có : \(x_1+x_2=\frac{1}{x_1}+\frac{1}{x_2}\Leftrightarrow x_1+x_2=\frac{x_1+x_2}{x_1x_2}\Leftrightarrow x_1x_2=1\)
\(x_1x_2=\frac{c}{a}=\frac{a^2-4a+1}{3}\)
Vậy ta có: \(a^2-4a+1=3\Leftrightarrow a^2-4a-2=0\Leftrightarrow\left[\begin{array}{nghiempt}a=2+\sqrt{6}\\a=2-\sqrt{6}\end{array}\right.\)

a, Ta có \(\Delta=\left(-3\right)^2-4.\left(-1\right).2=9+8=17>0\)
Nên pt có 2 nghiệm phân biệt
\(x_1=\frac{3-\sqrt{17}}{4};x_2=\frac{3+\sqrt{17}}{4}\)
b,A/D hệ thức vi et ta có
\(\hept{\begin{cases}x_1+x_2=\frac{3}{2}\\x_1x_2=-\frac{1}{2}\end{cases}}\)
ý cậu như nào >?

x1+x2=3; x1x2=-7
\(B=\left|x_1-x_2\right|=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}\)
\(=\sqrt{3^2-4\cdot\left(-7\right)}=\sqrt{37}\)
\(F=\left(x_1^2+x_2^2\right)^2-2\left(x_1\cdot x_2\right)^2\)
\(=\left[3^2-2\cdot\left(-7\right)\right]^2-2\cdot\left(-7\right)^2\)
\(=23^2-2\cdot49=431\)

xét ptr \(2x^2-x-3+0\)
△=\(\left(-1\right)^2-4.2.\left(-3\right)=25>0\)
⇒ptr có 2 ngh phân biệt \(x_1;x_2\)
Theo hệt thức viet \(x_1+x_2=\dfrac{1}{2};x_1x_2=\dfrac{-3}{2}\)
Xét A = \(x_1^2+x_2^2-x_1^2x_2^2=\left(x_1+x_2\right)^2-2x_1x_2-x_1^2x_2^2\)
=\(\left(\dfrac{1}{2}\right)^2-2\left(-\dfrac{3}{2}\right)-\left(-\dfrac{3}{2}\right)^2=\dfrac{1}{4}+3-\dfrac{9}{4}=3-2=1\)
Của cậu đây ạ, kh hiểu j thì hỏi tớ nha <3
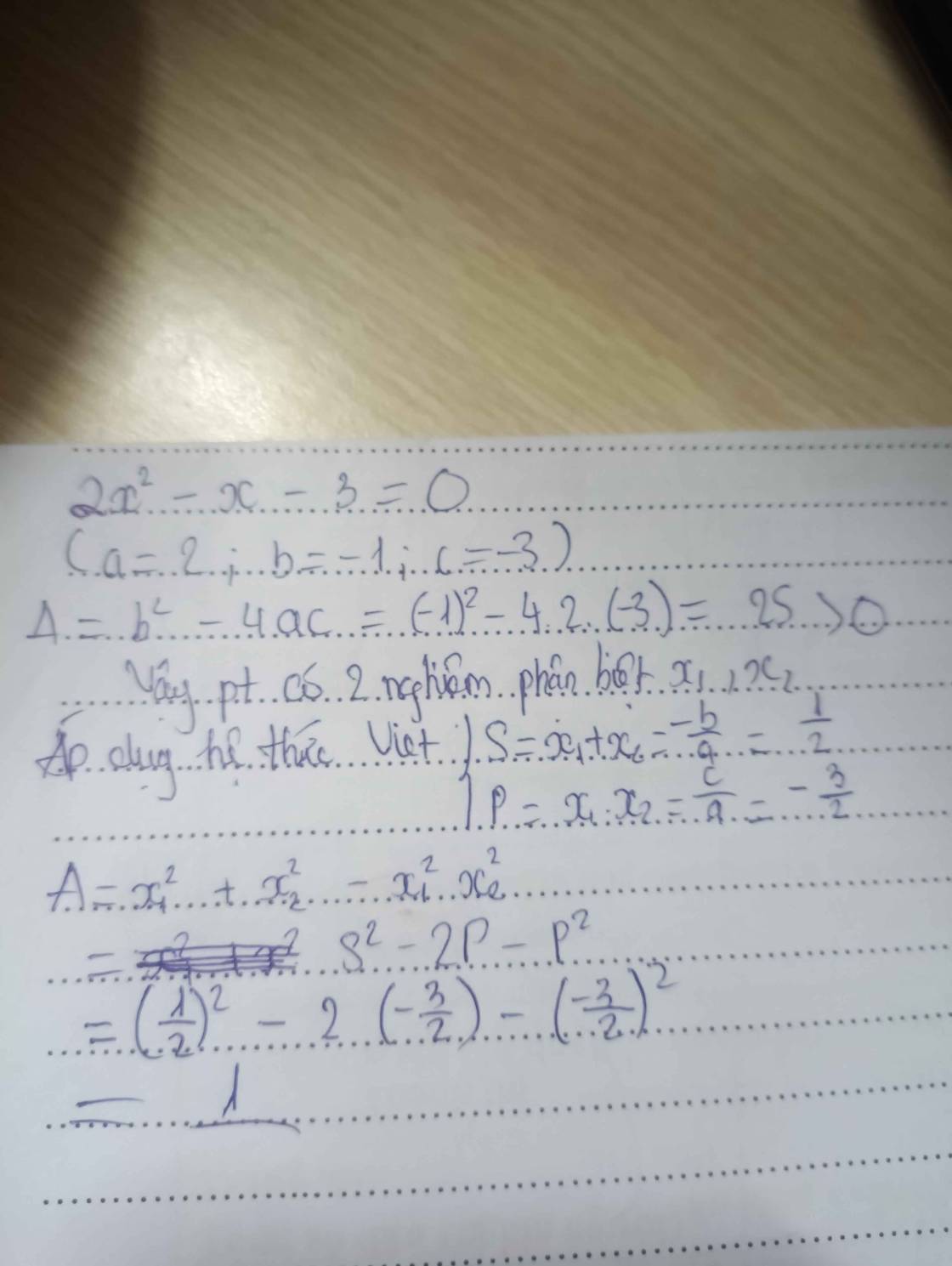
\(2x^2-3x-4=0\)
\(\Delta=3^2+4.2.4=41>0\)
⇒ Phương trình có hai nghiệm phân biệt
Theo Viét : \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{3}{2}\\x_1.x_2=-2\end{matrix}\right.\)
Lại có : \(A=\left(\dfrac{1}{x_1}\right)^2+\left(\dfrac{1}{x_2}\right)^2=\dfrac{1}{x_1^2}+\dfrac{1}{x_2^2}\)\(=\dfrac{x_1^2+x_2^2}{\left(x_1x_2\right)^2}=\dfrac{\left(x_1+x_2\right)^2-2x_1x_2}{\left(x_1x_2\right)^2}=\dfrac{\left(\dfrac{3}{2}\right)^2+4}{\left(-2\right)^2}=\dfrac{25}{16}\)
Vậy....