cho hcn ABCD vẽ đường cao BE của tam giác ABC
a, CM tam giác CEB đồng dạng với tam giác ABC
b, biết AB=25, AD= 20 tính be
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔCDA vuông tại D và ΔCEB vuông tại E có
góc C chung
Do đó: ΔCDA\(\sim\)ΔCEB
b: Xét ΔHEA vuông tại E và ΔHDB vuông tại D có
\(\widehat{AHE}=\widehat{BHD}\)
Do đó: ΔHEA\(\sim\)ΔHDB
Suy ra: HE/HD=HA/HB
hay \(HE\cdot HB=HD\cdot HA\)

a, ta có √(92+122)=15 nên theo định lý đảo của định lý pitago => ∠BAC=90 độ
Xét △ADB và △CAB có:
∠BAC=∠BDA(=90 độ), ∠ACB chung => △ADB ∼ △CAB (g.g) (1)
b, BE là đường phân giác của △ABC => \(\dfrac{AB}{AE}=\dfrac{BC}{EC}\)
Gọi AE= x (cm) => EC=12-x (cm)
Ta có: \(\dfrac{9}{x}=\dfrac{15}{12-x}\)=> 108-9x=15x =>108=24x => x=4,5
Vậy EA=4,5 cm, EC=12-4,5=7,5 cm
c, Xét △CAB và △CDA có:
∠BCD chung, ∠ADC=∠BAC(=90 độ) => △CAB ∼ △CDA (g.g) (2)
Từ (1),(2) => △ADB ∼ △CDA (T/c bắc cầu)
=> \(\dfrac{AD}{CD}=\dfrac{DB}{AD}\) => AD2=BD.DC
d, SABC=\(\dfrac{1}{2}.AB.AC\)=\(\dfrac{1}{2}AD.BC\)
=> AB.AC=AD.BC => AD = \(\dfrac{9.12}{15}\)=7,2 cm
Áp dụng định lí Pitago vào △ADC vuông tại D:
AC2=AD2+DC2 => DC=√[122-(7,2)2]=9,6 cm
=> BD=BC-DC=15-9,6=5,4 cm
BI là đường phân giác của △ABD => \(\dfrac{AB}{AI}=\dfrac{BD}{DI}\)
Gọi ID=y (cm) => AI=7,2-y (cm)
Ta có: \(\dfrac{9}{7,2-y}=\dfrac{5,4}{y}\)=> 9y=38,88-5,4y => 14,4y=38,88 => y = 2,7
Nên ID=2,7 cm

a: Xét tứ giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
=>góc BFE+góc BCE=180 độ
=>góc AFE=góc ACB
mà góc FAE chung
nên ΔAFE đồng dạng với ΔACB
b: Xét tứ giác BFHD có
góc BFH+goc BDH=180 độ
=>BFHD là tứ giác nội tiếp
Xét tứ giác CEHD có
góc CEH+góc CDH=180 độ
=>CEHD là tứ giác nội tiếp
góc FDH=góc FBH
góc EDH=góc ACF
mà góc FBH=góc ACF
nên góc FDH=góc EDH
=>DH là phân giác của góc FDE(1)
góc EFH=góc CAD
góc DFH=góc EBC
mà góc CAD=góc EBC
nên góc EFH=góc DFH
=>FH là phân giác của góc EFD(2)
Từ (1), (2) suy ra H là giao của ba đường phân giác của ΔDEF
c: Xét ΔBHD vuông tại D và ΔBCE vuông tại E có
góc HBD chung
=>ΔBHD đồg dạng với ΔBCE
=>BH/BC=BD/BE
=>BH*BE=BC*BD
Xét ΔCDH vuông tại Dvà ΔCFB vuông tại F có
góc FCB chung
=>ΔCDH đồng dạng với ΔCFB
=>CD/CF=CH/CB
=>CD*CB=CH*CF
=>BH*BE+CH*CF=BC^2

a: Xet ΔBAE vuông tại A và ΔBDF vuông tại D có
góc ABE=góc DBF
=>ΔBAE đồng dạng với ΔBDF
b: ΔABC vuông tại A có AD là đườg cao
nên BA^2=BD*BC
c: FD/FA=BD/BA
AE/CE=BA/BC
mà BD/BA=BA/BC
nên FD/FA=AE/CE

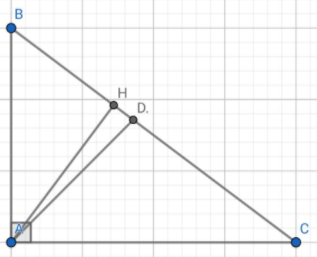
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
AH=6*8/10=4,8cm
BH=6^2/10=3,6cm

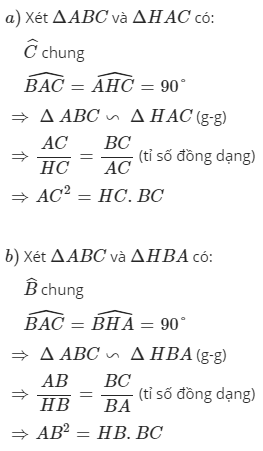

Mik copy trên mạng nên cs chút sai sót thì mog bn bỏ qua =)
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABH}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
b: Ta có: ΔABC\(\sim\)ΔHBA
nên \(\dfrac{AB}{HB}=\dfrac{CB}{AB}\)
hay \(AB^2=BH\cdot BC\)

Hình tự vẽ nha
xét tam giác ADB và tam giác ABC có
\(\widehat{ADB}=\widehat{ABC} (GT)\)
\(\widehat{A} chung\)
=> tam giác ADB đồng dạng vs tam giác ABC (g-g)
=> \(\dfrac{AD}{AB}=\dfrac{AB}{AC} (TSĐD)\)(1)
xét tam giác ABC có
AE là PG của góc A
E ∈ BC
=>\(\dfrac{EB}{EC}=\dfrac{AB}{AC} (TC \) tia pg trong tam giác) (2)
từ 1 và 2 =>\(\dfrac{AD}{AB}=\dfrac{EB}{EC}\)

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc HBA chung
=>ΔHBA đồng dạng với ΔABC
b; Xét ΔABE vuông tại A và ΔACB vuông tại A có
góc ABE=góc ACB
=>ΔABE đồng dạng với ΔACB
=>AB/AC=AE/AB
=>AB^2=AE*AC
c: Xét ΔBHD vuông tại H và ΔBAE vuông tại A có
góc HBD=góc ABE
=>ΔBHD đồng dạng với ΔBAE

a: Xét ΔCEB vuông tại E và ΔABC vuông tại B có
góc C chung
=>ΔECB đồng dạng với ΔBCA
b: \(AC=\sqrt{25^2+20^2}=5\sqrt{41}\left(cm\right)\)
\(BE=\dfrac{25\cdot20}{5\sqrt{41}}=\dfrac{100}{\sqrt{41}}\left(cm\right)\)