 giải câu 1;2;3;4 tự luận
giải câu 1;2;3;4 tự luận
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4:
b: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
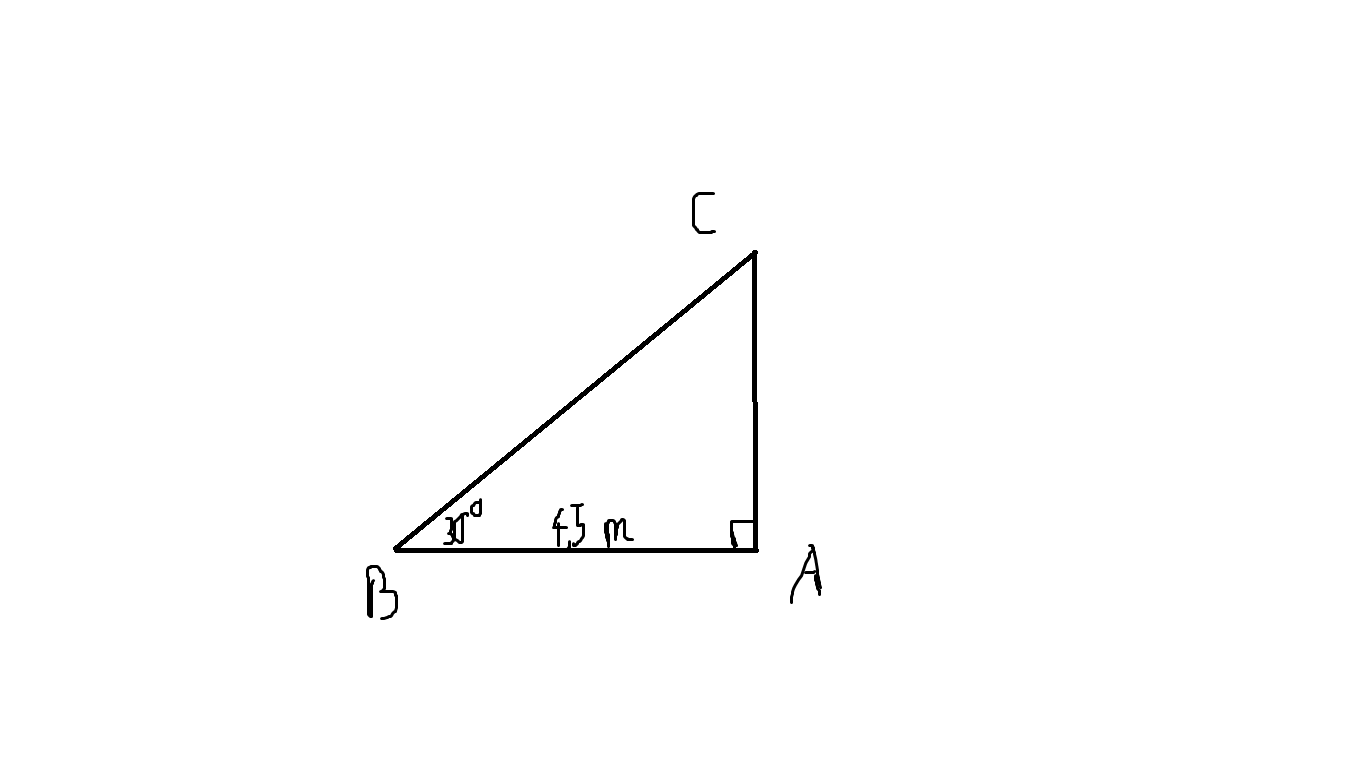
\(TanB=\dfrac{AC}{AB}\Rightarrow Tan30^o=\dfrac{AC}{4,5}\Rightarrow AC=Tan30^o.4,5=\dfrac{3\sqrt{3}}{2}\left(m\right)\)
\(CosB=\dfrac{AB}{BC}\Rightarrow Cos30^o=\dfrac{4,5}{BC}\Rightarrow BC=Cos30^o.4,5=\dfrac{9\sqrt{3}}{4}\)
Chiều cao ban đầu của cây tre là: \(\dfrac{3\sqrt{3}}{2}+\dfrac{9\sqrt{3}}{4}=\dfrac{15\sqrt{3}}{4}\approx6,5\left(m\right)\)

`1)a)5/9 + (-2)/9 = (5+(-2))/9 = 3/9 = 1/3`
`b)(-5)/9 : 10/3 = (-5)/9 . 3/10 = (-5.3)/(9.10) = (-15)/90 = (-1)/6`
`c)(-5)/4 + (-1)/3 +5/4 = (-5/4 + 5/4) + (-1)/3 = 0 + (-1)/3 = -1/3`
`d)(-2)/7 . 5/6 + (-2)/7 . 5/6 = (-2)/7 . ( 5/6 + 5/6 ) = (-2)/7 . 10/6 = (-2)/7 . 5/3 = (-2.5)/(7.3) = (-10)/24 = (-5)/12`
Gì đây mới câu 1 thôi, Còn câu 2,3,4,5 trên bài đâu, giải nhanh đây trước 14h05 trong ngày hôm nay nha.



2.
Áp dụng định lý hàm cosin:
\(b=\sqrt{a^2+c^2-2ac.cosB}=\sqrt{8^2+3^2-2.8.3.cos60^0}=7\)
\(S_{ABC}=\dfrac{1}{2}ac.sinB=\dfrac{1}{2}.8.3.sin60^0=6\sqrt{3}\)
4.
\(\Delta=\left(m+2\right)^2-16>0\Leftrightarrow m^2+4m-12>0\Rightarrow\left[{}\begin{matrix}m>2\\m< -6\end{matrix}\right.\) (1)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-m-2\\x_1x_2=4\end{matrix}\right.\)
\(x_1+x_2+x_1x_2>1\)
\(\Leftrightarrow-m-2+4>1\)
\(\Rightarrow m< 1\) (2)
Kết hợp (1); (2) ta được \(m< -6\)







1) \(7x-5=5x+20\)
⇔\(7x-5x=5+20\)
⇔ \(2x=25\)
⇔ \(x=\dfrac{25}{2}\)
Vậy tập nghiệm của phương trình S\(=\left\{\dfrac{25}{2}\right\}\)
2) \(3x-2=2x-3\)
⇔ \(3x-2x=2-3\)
⇔ \(x=-1\)
Vậy tập nghiệm của phương trình S \(=\left\{-1\right\}\)
4) \(\dfrac{7x-1}{6}-\dfrac{16-x}{5}=1\)
⇔ \(\dfrac{5\left(7x-1\right)}{30}-\dfrac{6\left(16-x\right)}{30}=\dfrac{30}{30}\)
⇔ \(\dfrac{35x-5}{30}-\dfrac{96-6x}{30}=\dfrac{30}{30}\)
⇒ \(35x-5-96+6x=30\)
⇔ \(35x+6x=5+96+30\)
⇔ \(41x=131\)
⇔ \(x=\dfrac{131}{41}\)
Vậy tập nghiệm của phương trình S \(=\left\{\dfrac{131}{41}\right\}\)
5) \(\left(3x+5\right)^2-\left(2x-3\right)^2=0\)
⇔\(\left(3x+5+2x-3\right)\left(3x+5-2x+3\right)=0\)
⇔ \(\left(5x+2\right)\left(x+8\right)=0\)
⇔ \(5x+2=0\) hoặc \(x+8=0\)
* \(5x+2=0\) * \(x+8=0\)
⇔\(5x\) \(=-2\) ⇔\(x\) \(=-8\)
⇔ \(x\) \(=\dfrac{-2}{5}\)
Vậy tập nghiệm của phương trình S \(=\left\{\dfrac{-2}{5},-8\right\}\)