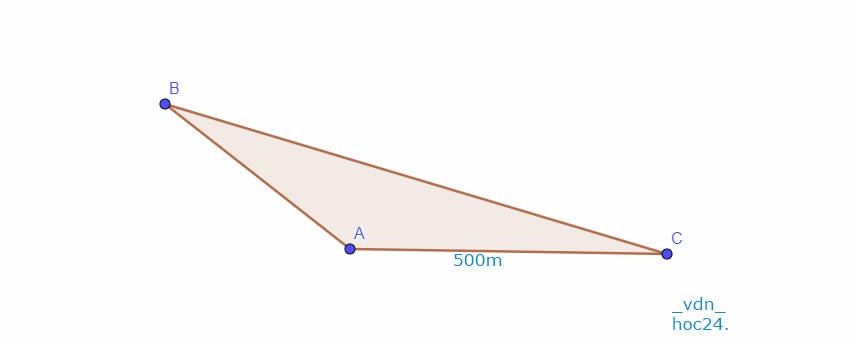
Ba địa điểm a b c lad 3 đỉnh của tam giác abc với a = 90 độ và khoảng cách giữa 2 địa điểm a và c là 550m người ta đặt một loa truyền thanh tại một địa điểm nằm giữa a và b thì tại c có thể nghe tiếng loa ko nếu bán kính để nghe rõ tiếng của loa là 550m
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


góc B>90 độ
=>góc BMA<90 độ
=>góc CMA>90 độ
=>CA>AM
=>AM<600
=>Ko thể nghe thấy đc

Vì \(\widehat{A} \) là góc tù `=>` Cạnh `BC` là cạnh lớn nhất
`=> BC > AC`
Mà bán kính nghe rõ của loa là `500m`
`=>` Từ khoảng cách đó không thể nghe thấy được.

Đổi: 1 km = 1000 m. Do đó AC = 1000 m.
Áp dụng định lí cosin trong tam giác ABC ta có:
\(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C\)
\(\begin{array}{l} \Rightarrow A{B^2} = {1000^2} + {800^2} - 2.1000.800.\cos {105^o}\\ \Rightarrow A{B^2} \approx 2054110,5\\ \Rightarrow AB \approx 1433,2\end{array}\)
Vậy khoảng cách AB là 1433,2 m.

Bài 2:
b: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
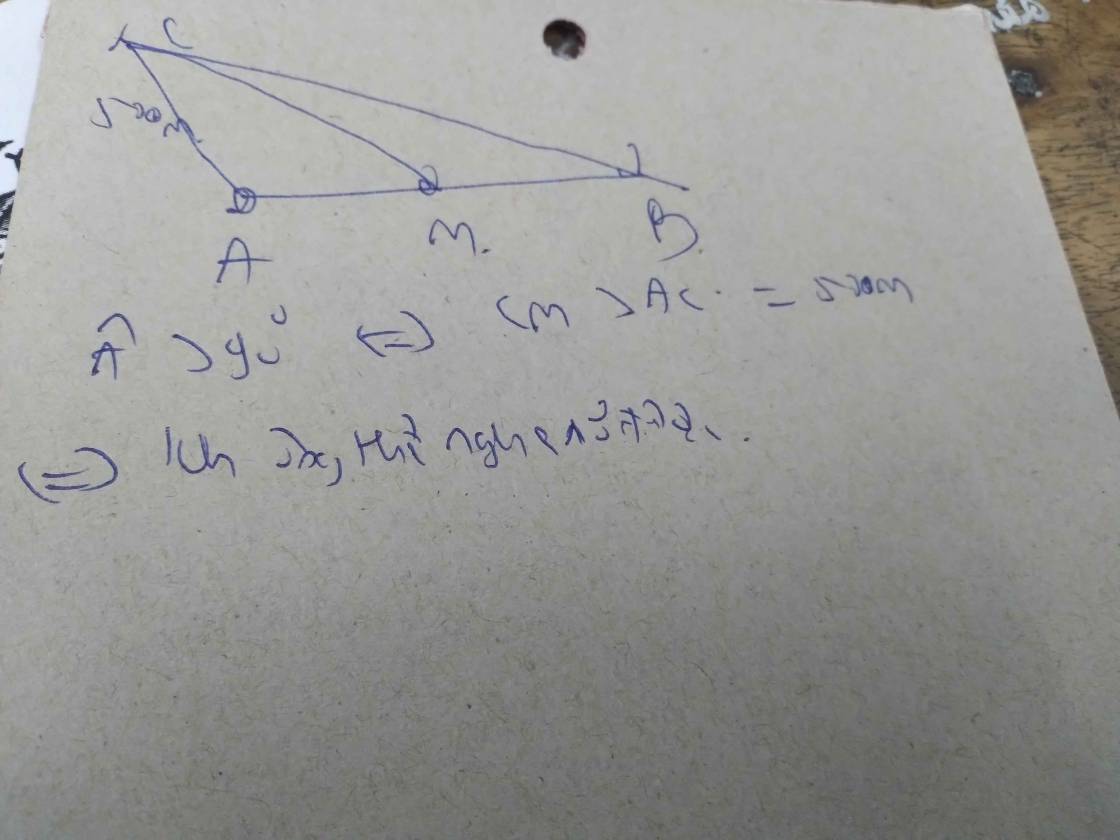
Gọi điểm được đặt là M
=>ΔAMC vuông tại A
=>AC<AM
=>Ko nghe rõ được bởi AM>550m
Gọi D là địa điểm đặt loa truyền thanh
Ta có: góc A=90°
=> AC là đường vuông góc
=> CD là đường xiên
Dó đó: AC<CD
Hay CD>550m( vì AC=550m )
Vậy tại C ko thể nghe rõ tiếng loa