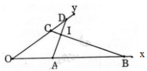
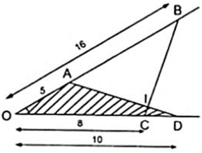
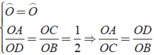Trên một cạnh của góc xOy khác 180⁰,đặt các đoạn thẳng OA=2,5cm OB=8cm.Trên cạnh thứ hai của góc đó ,đặt các đoạn thẳng OC=4cm OD=5cm A)Chứng minh hai tấm giác OCB và OAD đồng dạng B)Gọi giáo điểm của các cạnh AD và BC là I chứng minh rằng hai tấm giác IAB và ICD có các góc bằng nhau từng cặp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
16 tháng 3 2023
Đúng(0)
Những câu hỏi liên quan
15 tháng 6 2023
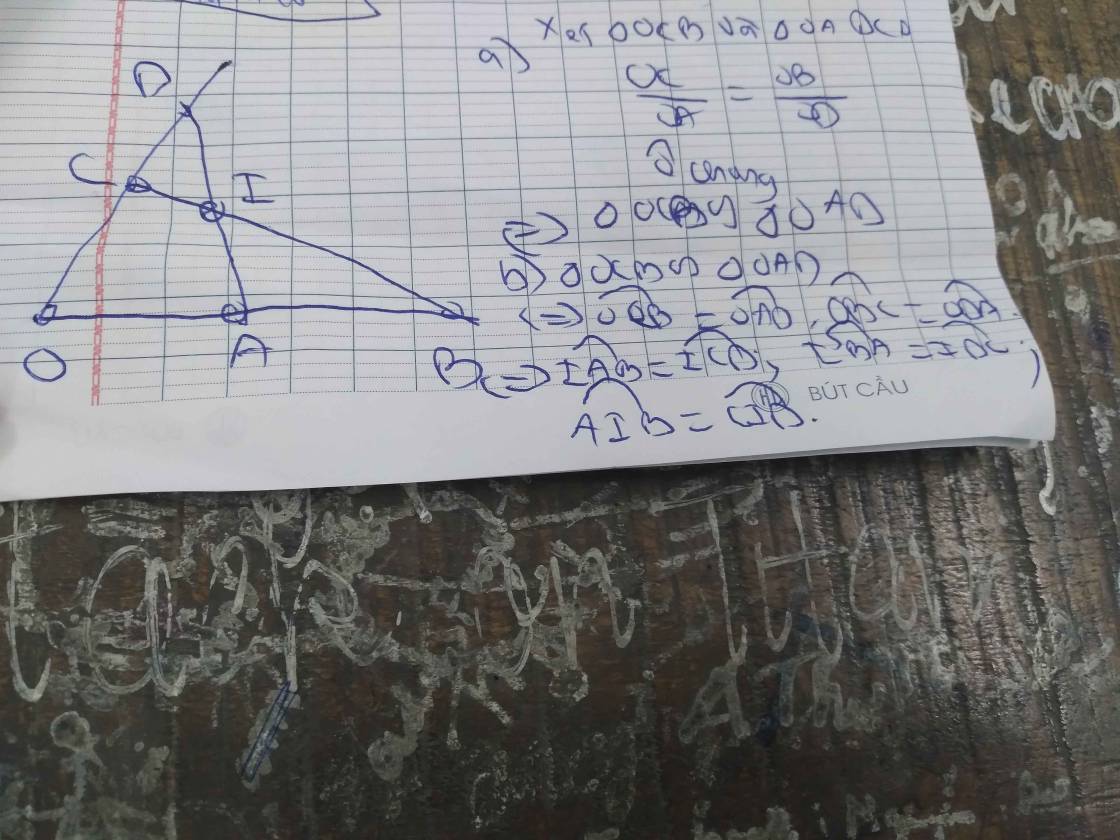
a:
| GT | góc xOy OA=5cm; OB=16cm; OC=8cm; OD=10cm |
| KL | ΔOBC đồng dạng với ΔOAD |
b: Xét ΔOCB và ΔOAD có
OC/OA=OB/OD
góc O chung
=>ΔOCB đồng dạng với ΔOAD
22 tháng 4 2017
Giả sử ∆A'B'C' ∽ ∆ABC, hiệu độ dài tương ứng của A'B' và AB là 12,5.
Ta có: = mà =
=> = => = = = = 6,25 cm
HS
27 tháng 2 2018
Giả sử ∆A'B'C' ∽ ∆ABC, hiệu độ dài tương ứng của A'B' và AB là 12,5.
Ta có: CABCCA′B′C′CABCCA′B′C′CABCCA′B′C′= 151715171517 mà CABCCA′B′C′CABCCA′B′C′CABCCA′B′C′ = ABA′B′ABA′B′ABA′B′
=> 151715171517 = ABA′B′ABA′B′ABA′B′ => AB15AB15AB15 = A′B′17A′B′17A′B′17 = A′B′−AB17−15A′B′−AB17−15A′B′−AB17−15 = 12.5212.5212.52 = 6,25 cm
HH
17 tháng 4 2020
a, Ta có :
\(\frac{OA}{OC}=\frac{5}{8};\frac{OB}{OD}=\frac{10}{16}=\frac{5}{8}\)
\(\Rightarrow\frac{OA}{OC}=\frac{OB}{OD}\)
Mà góc O chung nên \(\Delta OCB~\Delta OAD\)( trường hợp 2 )
b, \(\Delta ICD , \Delta IAB\)có :
\(\widehat{CID}=\widehat{AIB}\)( đối đỉnh )
\(\widehat{CDI}=\widehat{IBA} \left(do \Delta OCB~\Delta OAD\right)\)
\(\Rightarrow\widehat{DCI}=\widehat{BAI}\)( tổng 3 góc trong tam giác )
Vậy : Hai tam giác IAB và ICD có các góc = nhau từng đôi 1
