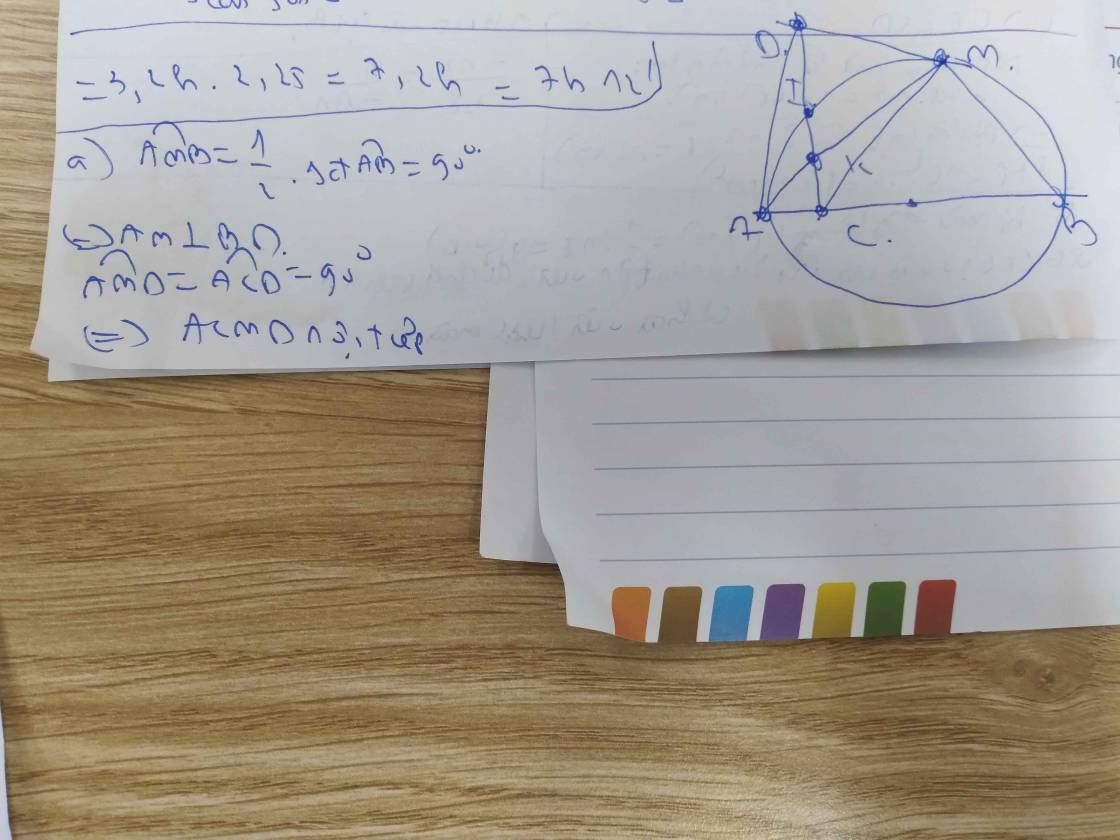
1/Cho nửa đường tròn (o) đường kính AB. C là 1 điểm bất kì trên nữa đường tròn sao cho C khác A và AC<CB điểm D thuộc cung nhỏ BC sao cho COD=90 độ. gọi E là gđ của AD và BC, F là gđ của AC vào BD
a) Chứng minh CEDF là tứ giác nội tiếp
b) Chứng minh FCEA là tứ giác nội tiếp
c) Gọi I là trung điểm của EF. chứng minh IC là tiếp tuyến của (o)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc ACB=1/2*180=90 độ
=>góc FCE=90 độ
góc ADB=1/2*180=90 độ
=>gó FDE=90 độ
Vì góc FCE+góc FDE=180 độ
nên FCED nội tiếp
b: Đề sai rồi bạn vì F,C,A thẳng hàng
c: góc ICO=góc ICE+góc OCE
=góc IEC+góc OBE
=90 độ-góc CBA+góc CBA
=90 độ
=>CI là tiếp tuyến của (O)

a: góc AEB=1/2*sđ cung AB=90 độ
Vì góc DHB+góc DEB=180 độ
nên DHBE nội tiếp
b: Xét ΔADC và ΔACE co
góc ACH=góc AEC(=góc ABC)
góc DAC chung
=>ΔADC đồng dạng với ΔACE
=>DC/EC=AD/AC
=>DC*AC=EC*AD

b: Xét (O) có
MC là tiếp tuyến
MA là tiếp tuyến
Do đó: MC=MA
Xét (O) có
NC là tiếp tuyến
NB là tiếp tuyến
Do đó: NC=NB
Ta có: MN=MC+NC
nên MN=MA+NB

a: góc ACB=góc ADB=1/2*180=90 độ
=>BC vuông góc AE,AD vuông góc BE
góc ECH+góc EDH=180 độ
=>ECHD nội tiếp
b: Xét ΔMBD và ΔMCB có
góc MBD=góc MCB
góc BMD chung
=>ΔMBD đồng dạng với ΔMCB
=>MB/MC=MD/MB
=>MB^2=MC*MD

a: Xét tứ giác OAMC có
\(\widehat{OAM}+\widehat{OCM}=180^0\)
Do đó: OAMC là tứ giác nội tiếp
a: góc ACB=1/2*180=90 độ
=>góc FCE=90 độ
góc ADB=1/2*180=90 độ
=>gó FDE=90 độ
Vì góc FCE+góc FDE=180 độ
nên FCED nội tiếp
b: Đề sai rồi bạn vì F,C,A thẳng hàng
c: góc ICO=góc ICE+góc OCE
=góc IEC+góc OBE
=90 độ-góc CBA+góc CBA
=90 độ
=>CI là tiếp tuyến của (O)