làm giúp em này vói ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(S_{Xq}=2\cdot pi\cdot2^2+\dfrac{1}{2}\cdot\sqrt{5}\cdot2=3\sqrt{5}\cdot pi\)

đổ nước vào hỗn hợp đó ta thấy muối sẽ hòa tan trong nước
lấy phần ko bị hòa tan ra đó là bột gỗ
đung cạn nước và thấy trong đó là muối


1)
- Dẫn hỗn hợp khí qua dd Ba(OH)2 dư, thu được kết tủa (1) và có khí (2) thoát ra
\(Ba\left(OH\right)_2+CO_2\rightarrow BaCO_3\downarrow+H_2O\)
\(Ba\left(OH\right)_2+SO_2\rightarrow BaSO_3\downarrow+H_2O\)
\(Ba\left(OH\right)_2+SO_3\rightarrow BaSO_4\downarrow+H_2O\)
- Lọc lấy kết tủa (1), hòa tan vào dd HCl dư, thấy có khí thoát ra (3) và chất rắn không tan => Trong hh khí ban đầu có SO3
\(BaCO_3+2HCl\rightarrow BaCl_2+CO_2+H_2O\)
\(BaSO_3+2HCl\rightarrow BaCl_2+SO_2+H_2O\)
- Dẫn khí (2) qua bột CuO đựng trong ống nghiệm, nung nóng, thấy chất rắn màu đen chuyển dần sang đỏ, có giọt nước tạo thành trong ống nghiệm => Trong hh khí ban đầu có H2
\(CuO+H_2\underrightarrow{t^o}Cu+H_2O\)
- Dẫn khí (3) qua dd Br2 dư, thấy dd nhạt màu dần, có khí thoát ra
=> Trong hh ban đầu có SO2 và khí thoát ra là CO2
\(Br_2+SO_2+2H_2O\rightarrow H_2SO_4+2HBr\)
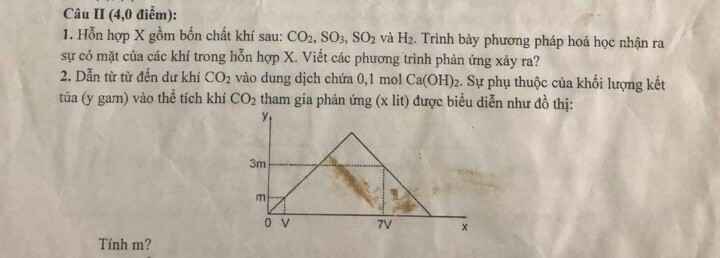
2)
Đặt \(n_{CO_2}=\dfrac{V}{22,4}\left(mol\right)=k\left(mol\right)\)
Đặt \(n_{CaCO_3}=\dfrac{m}{100}=n\left(mol\right)\)
- Khi cho k mol khí CO2, thu được n mol CaCO3, kết tủa không bị hòa tan
PTHH: Ca(OH)2 + CO2 --> CaCO3 + H2O
k-------->k
=> k = n (1)
- Khi cho 7k mol khí CO2, thu được 3n mol CaCO3, kết tủa bị hòa tan 1 phần
PTHH: Ca(OH)2 + CO2 --> CaCO3 + H2O
0,1------>0,1------->0,1
CaCO3 + CO2 + H2O --> Ca(HCO3)2
(7k-0,1)<--(7k-0,1)
=> 0,1 - (7k - 0,1) = 3n
=> 0,2 - 7k = 3n (2)
(1)(2) => k = 0,02; n = 0,02
Vậy m = 100n = 2 (g)


ĐK : x \(\ge-1\)
Ta có : \(x^2-2x-1=\sqrt{\left(x^2+1\right)\left(x+1\right)}\)
<=> \(\left(x^2+1\right)-2\left(x+1\right)=\sqrt{\left(x^2+1\right)\left(x+1\right)}\)
Đặt \(\sqrt{x^2+1}=a;\sqrt{x+1}=b\)(\(a>0;b\ge0\))
Khi đó a2 - 2b2 = ab
<=> (a - 2b)(a + b) = 0
<=> a - 2b = 0
<=> a = 2b
<=> \(\sqrt{x^2+1}=2\sqrt{x+1}\)
<=> \(\left\{{}\begin{matrix}x^2+1=4x+4\\x\ge-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-4x-3=0\\x\ge-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=\sqrt{7}+2\\x=-\sqrt{7}+2\end{matrix}\right.\\x\ge-1\end{matrix}\right.\Leftrightarrow x=\sqrt{7}+2\)



a: =>x=y+11
xy=60
=>y(y+11)=60
\(\Leftrightarrow y^2+15y-4y-60=0\)
=>(y+15)(y-4)=0
hay \(y\in\left\{-15;4\right\}\)



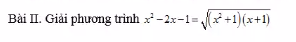


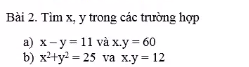
R=1/2CD=a
h=AD=2a
S1=Sxq=2*pi*r*h=2*pi*a*2a=4*pi*a^2
S2=Stp=2*pi*r^2+2*pi*r*h
=2*pi*a^2+2*pi*a*2a
=6*pi*a^2
>S1/S2=2/3