Câu 19. Một hộp có 5 cái thẻ có kích thước giống nhau và được đánh số lần lượt là 1; 2; 4; 7; 11. Rút ngẫu nhiên một thẻ trong hộp.
a) Viết tập hợp A gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.
b) Tính xác suất của các biến cố:
M : “ Rút được thẻ ghi số là số chẵn” ;
N : “ Rút được thẻ ghi số là số nguyên tố”.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) A = {1; 2; 4; 7; 11}
b) Xác suất của biến cố M:
2 : 5 . 100% = 40%
Xác suất của biến cố N:
3 : 5 . 100% = 60%

Vì 5 quả bóng có kích thước và khối lượng giống nhau nên 5 kết quả của phép thử có khả năng xảy ra bằng nhau.
- Biến cố \(A\) xảy ra khi ta lấy được quả bóng có số 5 hoặc 13 nên có 2 kết quả thuận lợi cho \(A\). Xác suất của biến có \(A\) là:
\(P\left( A \right) = \frac{2}{5}\).
- Vì không có quả bóng nào đánh số chia hết cho 3 nên số kết quả thuận lợi của biến cố \(B\) là 0. Xác suất của biến cố \(B\) là
\(P\left( B \right) = \frac{0}{5} = 0\).
- Vì cả 5 quả bóng đều đánh số lớn hơn 4 nên số kết quả thuận lợi của biến cố \(C\) là 5. Xác suất của biến cố \(C\) là
\(P\left( C \right) = \frac{5}{5} = 1\).

Do các tấm thẻ giống nhau, nên lấy 3 tấm từ 10 tấm không quan tâm thứ tự có \(C_{10}^3 = 120\)cách, suy ra \(n\left( \Omega \right) = 120\)
Gọi A là biến cố “Tích các số ghi trên ba thẻ đó là số chẵn”
Để tích các số trên thẻ là số chẵn thì ít nhất có 1 thẻ là số chẵn
Để chọn ra 3 thẻ thuận lợi cho biến cố A ta có 3 khả năng
+) Khả năng 1: 3 thẻ chọn ra có 1 thẻ có số chẵn và 2 thẻ có số lẻ có \(5.C_5^2 = 50\) khả năng
+) Khả năng 2: 3 thẻ chọn ra có 2 thẻ có số chẵn và 1 thẻ có số lẻ có \(C_5^2.5 = 50\) khả năng
+) Khả năng 3: 3 thẻ chọn ra có đều là có số chắn có \(C_5^3 = 10\) khả năng
Suy ra \(n\left( A \right) = 50 + 50 + 10 = 110\)
Vậy xác suất của biến cố A là: \(P(A) = \frac{{110}}{{120}} = \frac{{11}}{{12}}\)

a) Các kết quả có thể xảy ra trong 2 lần lấy tấm thẻ từ 2 hộp được thể hiện ở sơ đồ hình cây như hình dưới đây:
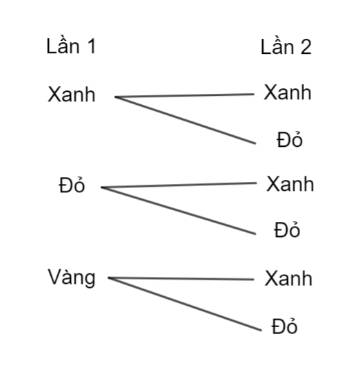
b)
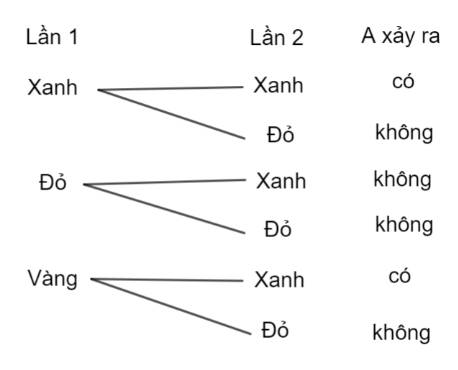
Gọi A là biến cố “Trong 2 thẻ lấy ra không có thẻ màu đỏ nào” là biến cố đối của biến cố “Trong 2 thẻ lấy ra có ít nhất 2 thẻ màu đỏ”
Dựa vào sơ đồ hình cây ta thấy có tất cả 6 kết quả có thể xảy ra, trong đó có 2 kết quả thuận lợi cho I. Do đó: \(P(A) = \frac{2}{6} = \frac{1}{3}\)
Vậy xác suất của biến cố “Trong 2 thẻ lấy ra có ít nhất 2 thẻ màu đỏ” là \(1 - \frac{1}{3} = \frac{2}{3}\)

THAM KHẢO:
A = {(2;1);(2;2);(2;3);(2;4);(2;5);(4;1);(4;2);(4;3);(4;4);(4;5)}
B = {(1;2);(2;2);(3;2);(4;2);(5;2);(1;4);(2;4);(3;4);(4;4);(5;4)}
C = {(1;2);(1;4);(2;1);(2;2);(2;3);(2;4);(2;5);(3;2);(3;4);(4;1);(4;2);(4;3);(4;4);(4;5); (5;2);(5;4)}

1.
\(\left|\Omega\right|=15\)
a, \(P\left(A\right)=\dfrac{7}{15}\)
b, \(P\left(B\right)=\dfrac{2}{5}\)
c, \(P\left(C\right)=\dfrac{3}{5}\)
2.
\(\left|\Omega\right|=C^5_{18}\)
a, \(\left|\Omega_A\right|=C^5_5+C^5_6+C^5_7\)
\(P\left(B\right)=\dfrac{C^5_5+C^5_6+C^5_7}{C^5_{18}}=\dfrac{1}{306}\)
b, TH1: 2 bi đỏ, 1 bi xanh, 2 bi vàng
\(\Rightarrow\) Có \(C^2_6.C^1_5.C^2_7\) cách lấy.
TH2: 2 bi đỏ, 2 bi xanh, 1 bi vàng
\(\Rightarrow\) Có \(C^2_6.C^2_5.C^1_7\) cách lấy.
\(\Rightarrow\left|\Omega_C\right|=C^2_6.C^1_5.C^2_7+C^2_6.C^2_5.C^1_7\)
\(\Rightarrow P\left(C\right)=\dfrac{C^2_6.C^1_5.C^2_7+C^2_6.C^2_5.C^1_7}{C^5_{18}}=\dfrac{10}{51}\)
c, \(\overline{D}\) là biến cố không lấy ra bi xanh nào.
\(\left|\Omega_{\overline{D}}\right|=C^5_{13}\)
\(\Rightarrow P\left(\overline{D}\right)=\dfrac{C^5_{13}}{C^5_{18}}=\dfrac{143}{952}\)
\(\Rightarrow P\left(D\right)=1-\dfrac{143}{952}=\dfrac{809}{952}\)
Lời giải:
a. $A=\left\{1;2;4;7;11\right\}$
b.
Rút ngẫu nhiên 1 thẻ từ hộp, có 5 khả năng (1,2,4,7,11)
Rút được thẻ ghi số chẵn, tức là rút phải thẻ $2,4$ (2 khả năng)
Rút được thẻ ghi số nguyên tố, tức là rút phải thẻ $2,7,11$ (3 khả năng)
Xác suất để biến cố M xảy ra: $\frac{2}{5}$
Xác suất để biến cố N xảy ra: $\frac{3}{5}$