Cho ΔABC có AB=AC. Lấy điểm E trên cạnh AB, F trên cạnh AC sao cho AE=AF.
a) Chứng minh: BF=CE và ΔBEC=ΔCFB.
b) BF cắt CE tại I. CMR: ΔIBE=ΔICF.
c) CMR: AI là tia phân giác của \(\widehat{BAC}\).
d) Gọi M là trung điểm của BC. CMR: A, I, M thẳng hàng.

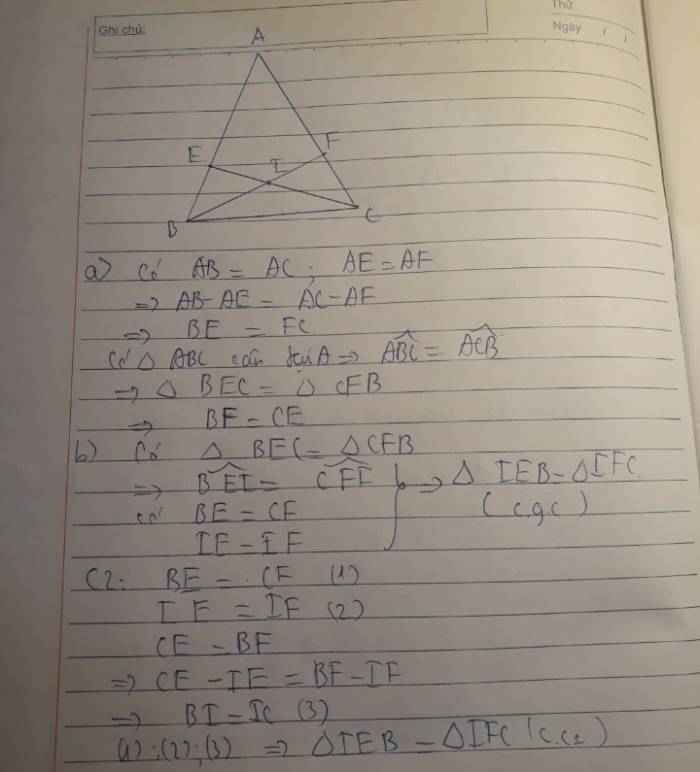
a: Xét ΔEBC và ΔFCB có
EB=FC
góc EBC=góc FCB
BC chung
=>ΔEBC=ΔFCB
=>EC=FB
b: Xét ΔIBC có góc IBC=góc ICB
nên ΔICB cân tại I
=>IB=IC
Xét ΔIBE và ΔICF có
IB=IC
IE=IF
BE=CF
=>ΔIBE=ΔICF
c: Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
=>ΔAIB=ΔAIC
=>góc IAB=góc IAC
=>AI là phân giáccủa góc BAC