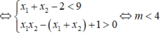Cho phương trình: \(2x^2-6x+m+7=0\)
a. Giải phương trình với \(m=3\)
b. Với giá trị nào của m thì phương trình có một trong các nghiệm bằng - 4
c. Tìm m để phương trình có hai nghiệm \(x1,x2\) thõa mãn điều kiện \(x1=-2x^2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 8 2019
a) Với m= 2, ta có phương trình: x 2 + 2 x − 3 = 0
Ta có: a + b + c = 1 + 2 − 3 = 0
Theo định lý Viet, phương trình có 2 nghiệm:
x 1 = 1 ; x 2 = − 3 ⇒ S = 1 ; − 3 .
b) Chứng minh rằng phương trình luôn có nghiệm ∀ m .
Ta có: Δ ' = m − 1 2 − 1 + 2 m = m 2 ≥ 0 ; ∀ m
Vậy phương trình luôn có nghiệm ∀ m .
c) Theo định lý Viet, ta có: x 1 + x 2 = − 2 m + 2 x 1 . x 2 = 1 − 2 m
Ta có:
x 1 2 . x 2 + x 1 . x 2 2 = 2 x 1 . x 2 + 3 ⇔ x 1 . x 2 x 1 + x 2 − 2 = 6 ⇒ 1 − 2 m − 2 m + 2 − 2 = 6 ⇔ 2 m 2 − m − 3 = 0
Ta có: a − b + c = 2 + 1 − 3 = 0 ⇒ m 1 = − 1 ; m 2 = 3 2
Vậy m= -1 hoặc m= 3/2
23 tháng 6 2021
a) Pt có hai nghiệm trái dấu \(\Leftrightarrow ac< 0\Leftrightarrow m< 0\)
b) Pt có nghiệm khi \(\Delta\ge0\Leftrightarrow36-4m\ge0\Leftrightarrow m\le9\)
Áp dụng hệ thức viet có:
\(\left\{{}\begin{matrix}x_1+x_2=6\left(1\right)\\x_1x_2=m\left(2\right)\end{matrix}\right.\)
Từ (1) kết hợp với điều kiện có:\(\left\{{}\begin{matrix}x_1+x_2=6\\x_1-2x_2=m\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}3x_2=6-m\\x_1+x_2=6\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{6-m}{3}\\x_1=6-x_2=\dfrac{12+m}{3}\end{matrix}\right.\)
\(\Rightarrow x_1x_2=\dfrac{6-m}{3}.\dfrac{12+m}{3}=m\)
\(\Leftrightarrow72-15m-m^2=0\)
\(\Delta=3\sqrt{57}\)
\(\Rightarrow m=\dfrac{-15\pm3\sqrt{57}}{2}\) (thỏa mãn)
Vậy...
23 tháng 2 2022
1: Để phương trình có hai nghiệm trái dấu thì m<0
2: Để phương trình có hai nghiệm thì Δ>=0
=>36-4m>=0
=>m<=9
Theo đề, ta có:
\(\left\{{}\begin{matrix}x_1-x_2=4\\x_1+x_2=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=5\\x_2=1\end{matrix}\right.\)
Theo đề, ta có: \(x_1x_2=m\)
=>m=5(nhận)
23 tháng 2 2022
a, Thay m=0 vào pt ta có:
\(x^2-x+1=0\)
\(\Rightarrow\) pt vô nghiệm
b, Để pt có 2 nghiệm thì \(\Delta\ge0\)
\(\Leftrightarrow\left(-1\right)^2-4.1\left(m+1\right)\ge0\\ \Leftrightarrow1-4m-4\ge0\\ \Leftrightarrow-3-4m\ge0\\ \Leftrightarrow4m+3\le0\\ \Leftrightarrow m\le-\dfrac{3}{4}\)
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=m+1\end{matrix}\right.\)
\(x_1x_2\left(x_1x_2-2\right)=3\left(x_1+x_2\right)\\ \Leftrightarrow\left(x_1x_2\right)^2-2x_1x_2=3.1\\ \Leftrightarrow\left(m+1\right)^2-2\left(m+1\right)-3=0\\ \Leftrightarrow\left[{}\begin{matrix}m+1=3\\m+1=-1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}m=2\left(ktm\right)\\m=-2\left(tm\right)\end{matrix}\right.\)
4 tháng 4 2021
a) Thay x=0 vào phương trình, ta được:
\(4\cdot0^2-2\cdot\left(2m+3\right)\cdot0+m+1=0\)
\(\Leftrightarrow m+1=0\)
hay m=-1
Áp dụng hệ thức Vi-et, ta có:
\(x_1+x_2=\dfrac{2\left(2m+3\right)}{4}\)
\(\Leftrightarrow x_1=\dfrac{2\cdot\left(-2+3\right)}{4}=\dfrac{2}{4}=\dfrac{1}{2}\)
Vậy: Khi m=-1 và nghiệm còn lại là \(x=\dfrac{1}{2}\)
7 tháng 1 2023
Δ=(-2)^2-4(m-3)
=4-4m+12=-4m+16
Để pt có hai nghiệm thì -4m+16>=0
=>-4m>=-16
=>m<=4
x1^2+x2^2-x1x2<7
=>(x1+x2)^2-3x1x2<7
=>2^2-3(m-3)<7
=>4-3m+9<7
=>-3m+13<7
=>-3m<-6
=>m>2
=>2<m<=4
14 tháng 7 2023
a: Khi m=-2 thì (1) sẽ là;
x^2+2x-3=0
=>x=-3 hoặc x=1
b: Δ=(-m)^2-4(m-1)
=m^2-4m+4=(m-2)^2>=0
=>Phương trình luôn có 2 nghiệm
c: (1) có 1 nghiệm bằng 3
=>3^2-3m+m-1=0
=>8-2m=0
=>m=4
=>x^2-4x+3=0
=>x=1 hoặc x=3
Vậy: nghiệm còn lại là 1
CM
10 tháng 8 2018
a) Với m = 1 phương trình trở thành:
x 2 + 4x + 4 = 0 ⇔ (x + 2 ) 2 = 0 ⇔ x = -2
Vậy x = -2
b) Ta có: Δ' = m 2 - 5m + 4
Phương trình có hai nghiệm phân biệt
⇔ Δ' > 0 ⇔
m
2
- 5m + 4 > 0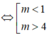 
Do x1 < x2 < 1
