Cho tam giác ABC, các đường trung tuyến BD và CE.
Chứng minh rằng: BD + CE > 3/2.BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi G là giao điểm của BD và CE. Dựa theo bất đẳng thức của tam giác
Vì GB+GC>BC=10(T/C của tam giác)
=>2/3BD+2/3CE>10 cm
=>BD+CE>3/2.10=15cm(dpcm)
lớp 5B trồng được nhiều hơn lớp 5A là 5 cây. Biết rằng mỗi bạn lớp 5A trồng 3 cây thì lớp đó thừa 2 cây -> Nếu mỗi bạn lớp 5B trồng 3 cây thì lớp đó thừa 7 cây.
Vẽ sơ đồ cho lớp 5B :
3 phần + 7 cây
=
4 phần - 38 cây
Từ đó suy ra một phần có giá trị 38 + 7 = 45, chính là số h/s của lớp 5B = số h/s của lớp 5A
số cấy của lớp 5a là 3*45-2 =133 cấy
số cây lớp 5b là 3*45-7= 128

Bài làm
Xét tam giác ABC có:
BD và CE cắt nhau ở G
Mà BD và CE là các đường trung tuyến
=> G là trọng tâm của tam giác ABC
Theo tính chất đường trung tuyến có:
\(\frac{BD}{BG}=\frac{3}{2}\Rightarrow BD=\frac{3}{2}BG\) (1)
\(\frac{CE}{CG}=\frac{3}{2}\Rightarrow CE=\frac{3}{2}CG\) (2)
Cộng (1) vào (2) ta được:
\(BD+CE=\frac{3}{2}BG+\frac{3}{2}CG\)
=> \(BD+CE=\frac{3}{2}\left(BG+CG\right)\)
=> \(BD+CE=\frac{3}{2}\left(BG+CG\right)\)
=> \(\left(BD+CE\right):\frac{3}{2}=BG+CG\)
=>\(\frac{2}{3}\left(BD+CE\right)=BG+CG\) (3)
Xét tam giác GBC có:
BG + CG > BC ( theo bất đẳng thức của tam giác )
=> \(\frac{2}{3}\left(BG+CE\right)>BC\) (4)
Từ (3) và (4) => BD + CE > BC : 2/3
=> BD + CE > 3/2BC
Chả biết mik đúng hay do đề sai. Đã thế lại cho BC mặc dù không cần. Đề sai hay thiếu à ?

Xét tam giác ABC : BD-đường trung tuyến
CE-đường trung tuyến
BD cắt CE tại G
=> G - trọng tâm tam giác ABC.
=> BG=2/3 BD
=>CE=2/3 CE
Xét tam giác BGC
=> BG+CG > BC ( BĐT trong tam giác)
=>2/3 BD +2/3 CE > BC
=> 2/3 (BD+CE ) > BC
Thay số : BC=8 cm ta đc :
2/3(BD+CE) > 8cm
=> 3/2 . 2/3 (BD+CE)> 3/2 . 8cm
=> BD+CE > 12cm

Gọi G là giao điểm của BD và CE.
Trong ∆GBC, ta có:
GB + GC > BC (bất đẳng thức tam giác)
GB = 2/3 BD (tính chất đường trung tuyến)
GC = 2/3 CE (tính chất đường trung tuyến)
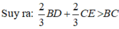
Mà BC = 10 cm (gt)
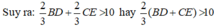
⇒ BD + CE > 15 (cm).

a) ΔABC có 2 đường trung tuyến BD; CE
G là trọng tâm
=> BG/BD = 2/3
CG/CE = 2/3
b) Trong tam giác BGC ta có: BG + GC > BC
=> 2/3DB + 2/3CE > BC (G là trọng tâm)
=> 2/3(DB + CE) > BC
=> 3/2. 2/3 (DB+CE)> 3/2BC
=> (DB + CE)>3/2BC
Gọi giao điểm của BD và CE là G.
\(\Rightarrow\hept{\begin{cases}BD=\frac{3}{2}BG\\CE=\frac{3}{2}CG\end{cases}}\)
\(\Rightarrow BD+CE=\frac{3}{2}\left(BG+CG\right)\)
Xét tam giác BGC có BG + CG > BC ( bất đẳng thức trong tam giác)
\(\Rightarrow BD+CE>\frac{3}{2}BC\)